Question

16．在△ABC中，已知AB=1，AC=$\frac{{\sqrt{3}}}{2}$，∠ABC=45°，求△ACB的面积．

Answer 1

分析 过A作AD⊥BC，交BC（或BC延长线）于点D，利用勾股定理和三角形的面积公式分别求出S_△ABD和S_△ACD，再分∠C为锐角和钝角两种情况求出S_△ACB即可．

解答 解：过A作AD⊥BC，交BC（或BC延长线）于点D，如图所示．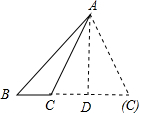
在Rt△ABD中，AD=BD=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$，
在Rt△ACD中，AC=$\frac{\sqrt{3}}{2}$，AD=$\frac{\sqrt{2}}{2}$，
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\frac{1}{2}$，
∴S_△ABD=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{4}$，S_△ACD=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{8}$．
∴当∠C为锐角时，S_△ACB=S_△ABD+S_△ACD=$\frac{2+\sqrt{2}}{8}$；当∠C为钝角时，S_△ACB=S_△ABD-S_△ACD=$\frac{{2-\sqrt{2}}}{8}$．

点评 本题考查了勾股定理以及三角形的面积，分∠C为锐角和钝角两种情况找出△ACB的面积是解题的关键．