题目内容
20.一次函数y1=x-1与反比例函数${y_2}=\frac{k}{x}$图象的一个交点为A(-1,m ).(1)求k和m的值;
(2)判断点B(2,1)是否为这两个函数图象的一个交点,并说明理由;
(3)当y1>y2时,请直接写出y2的范围.
分析 (1)先把点A(-1,m )代入一次函数y1=x-1,求出m的值故可得出A点坐标,再把A点坐标代入反比例函数${y_2}=\frac{k}{x}$,求出k的值即可;
(2)把点B(2,1)分别代入两个函数的解析式进行检验即可;
(3)在同一坐标系内画出两个函数图象,利用数形结合即可得出结论.
解答 解:(1)∵一次函数y1=x-1与反比例函数${y_2}=\frac{k}{x}$图象的一个交点为A(-1,m ).
∴m=-1-1=-2,
∴k=(-1)×(-2)=2;
(2)∵当x=2时,y1=x-1=1,
∴点B在y1=x-1的图象上.
∵当x=2时,y2=$\frac{2}{x}$=1,
∴点B在y2=$\frac{2}{x}$的图象上,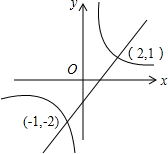
∴点B(2,1)是这两个函数图象的一个交点;
(3)∵由题意可得,$\left\{\begin{array}{l}{y}_{1}=x-1\\{y}_{2}=\frac{2}{x}\end{array}\right.$,解得$\left\{\begin{array}{l}x=-1\\ y=-2\end{array}\right.$或$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$,
∴两函数图象如图所示,
由图可知,当y1>y2时,y2<-2或0<y2<1.
点评 本题考查的是反比例函数的图象与一次函数图象的交点问题,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
10.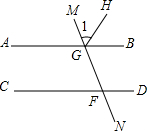 如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )
如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )
 如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )
如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
8. 如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )
如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )
 如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )
如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )| A. | 22° | B. | 34° | C. | 56° | D. | 78° |
15.有四个式子:①$\sqrt{18}=3\sqrt{2}$;②$\sqrt{9}=±3$;③${(\sqrt{5}+1)^2}=6$;④3a3•2a2=6a6,从这四个式子中随机抽取一个,抽到的式子不正确的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可)
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可) 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D.
如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D. 如图,等边三角形ABC中,ED=DF,∠EDF=60°,求证:BC=BE+CF.
如图,等边三角形ABC中,ED=DF,∠EDF=60°,求证:BC=BE+CF.