题目内容
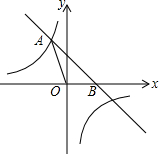 如图,直线y=-x+2与反比例函数y=
如图,直线y=-x+2与反比例函数y=| k |
| x |
(1)求该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积是△AOB的面积的
| 2 |
| 3 |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A的坐标代入直线的解析式就可求得a,然后把(-1,3)代入y=
的就可求得k,从而求得反比例函数的解析式;
(2)先求得三角形AOB的面积,然后求得三角形AOP的面积,进而求得P的纵坐标,从而求得P的坐标.
| k |
| x |
(2)先求得三角形AOB的面积,然后求得三角形AOP的面积,进而求得P的纵坐标,从而求得P的坐标.
解答:解:(1)∵点A(a,3)在直线y=-x+2上,
∴3=-a+2.
∴a=-1.
∴A(-1,3).
∵点A(-1,3)在反比例函数y=
的图象上,
∴3=
.
∴k=-3.
∴该反比例函数的表达式y=-
.
(2)直线y=-x+2与x轴相交于点B.
∴B(2,0),
∴S△AOB=
×2×3=3,
∵△AOP的面积是△AOB的面积的
,
∴S△AOP=2,
设P(0,n),
∴S△AOP=
×|n|×|-1|=2,
∴|n|=4,
∴n=±4,
∴P的坐标为(0,4 )或(0,-4 ).
∴3=-a+2.
∴a=-1.
∴A(-1,3).
∵点A(-1,3)在反比例函数y=
| k |
| x |
∴3=
| k |
| -1 |
∴k=-3.
∴该反比例函数的表达式y=-
| 3 |
| x |
(2)直线y=-x+2与x轴相交于点B.
∴B(2,0),
∴S△AOB=
| 1 |
| 2 |
∵△AOP的面积是△AOB的面积的
| 2 |
| 3 |
∴S△AOP=2,
设P(0,n),
∴S△AOP=
| 1 |
| 2 |
∴|n|=4,
∴n=±4,
∴P的坐标为(0,4 )或(0,-4 ).
点评:本题考查了一次函数与反比例函数的综合应用,重点是正确利用待定系数法求得函数的解析式.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知两圆半径分别是3和4,若两圆内切,则两圆的圆心距为( )
| A、1或7 | B、1 | C、7 | D、2 |
下列四个交通标志中,轴对称图形是( )
A、 |
B、 |
C、 |
D、 |
将抛物线y=(x-1)2向左平移2个单位,所得抛物线的表达式为( )
| A、y=(x+1)2 |
| B、y=(x-3)2 |
| C、y=(x-1)2+2 |
| D、y=(x-1)2-2 |
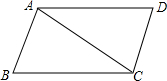 如图,在四边形ABCD中,AD∥BC,如果添加下列条件,不能使得△ABC∽△DCA成立的是( )
如图,在四边形ABCD中,AD∥BC,如果添加下列条件,不能使得△ABC∽△DCA成立的是( )| A、∠BAC=∠ADC | ||||
| B、∠B=∠ACD | ||||
| C、AC2=AD•BC | ||||
D、
|
 如图,A、B两点在双曲线y=
如图,A、B两点在双曲线y=