题目内容
6.关于x的方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )| A. | m≤2 | B. | m<2 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
分析 分二次项系数m-1≠0和m-1=0两种情况考虑,当m-1≠0时,根据根的判别式△≥0可得出关于m的一元一次不等式,解不等式即可得出m的取值范围;当m-1=0时,可得出方程有一个实数根.结合两种情况即可得出结论.
解答 解:①当m-1≠0,即m≠1时,
∵关于x的方程(m-1)x2+2x+1=0有实数根,
∴△=22-4×(m-1)×1=8-4m≥0,
解得:m≤2.
②当m-1=0,即m=1时,原方程为2x+1=0,
该方程有一个实数根.
综上可知:m的取值范围是m≤2.
故选A.
点评 本题考查了根的判别式,解题的关键是分两种情况考虑.本题属于基础题,难度不大,解决该题型题目时,分方程为一元二次方程和一元一次方程两种情况考虑是关键.

练习册系列答案
相关题目
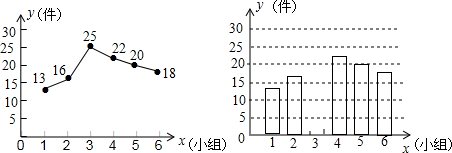
17.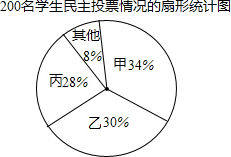 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:| 试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
14. 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
| 品种 | 今年成活棵树 | 成活率 |
| A | 540 | 90% |
| B | a | 96% |
| C | 368 | 92% |
| 合计 | 1388 |
11. 如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
 如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )
如图,正三角形ABC是⊙O的内接三角形,点P是劣弧AB上不同于点A、B的任意一点,则∠BPC的度数是( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
18.下列计算中正确的是( )
| A. | -1-1=0 | B. | 32=6 | C. | -2÷$\frac{1}{2}$=-1 | D. | -33-(-3)3=0 |
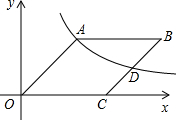 如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.
如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.