题目内容
10.计算:(1)-12-(1-0.5)×$\frac{1}{3}$×$\sqrt{36}$
(2)(8a2b-5ab2)-2(3a2b-4ab2)
(3)9(3-x)2=25
(4)$\left\{\begin{array}{l}{2x-y=5}\\{3x+4y=2}\end{array}\right.$.
分析 (1)原式第一项利用乘方的意义化简,第二项利用算术平方根的定义及乘法法则计算即可得到结果;
(2)原式去括号合并即可得到结果;
(3)方程开方即可求出解;
(4)方程组利用加减消元法求出解即可.
解答 解:(1)原式=-1-$\frac{1}{2}$×$\frac{1}{3}$×6=-1-1=-2;
(2)原式=8a2b-5ab2-6a2b+8ab2=2a2b+3ab2;
(3)方程开方得:3(3-x)=5或3(3-x)=-5,
解得:x1=-$\frac{4}{3}$,x2=$\frac{14}{3}$;
(4)$\left\{\begin{array}{l}{2x-y=5①}\\{3x+4y=2②}\end{array}\right.$,
①×4+②得:11x=22,即x=2,
把x=2代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 此题考查了实数的运算,以及整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.以下列各组数作为三角形的边长,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 6,8,11 | C. | 1,1,$\sqrt{2}$ | D. | 5,12,23 |
18.已知x,y为实数,且|4x-y-2|+(2x+y-10)2=0,则( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=-6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=6}\end{array}\right.$ |
5.有下列说法:(1)无理数就是开方开不尽的数;(2)无理数是无限不循环小数;(3)无理数包括正无理数、零、负无理数;(4)无理数都可以用数轴上的点来表示.其中正确的说法的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.在图示的汽车标志图案中,能用平移变换(不考虑颜色)来分析其形成过程的图案有( )

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.已知二次函数y=$\frac{1}{4}$(x-h)2+4,当x>-1时,y随x的增大而增大,则有( )
| A. | h≥-1 | B. | h>-1 | C. | h<-1 | D. | h≤-1 |
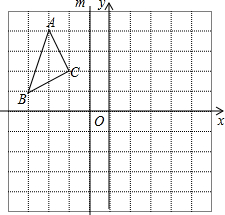 在如图所示的正方形网格中,已知△ABC的三个顶点分别是格点A、B、C.
在如图所示的正方形网格中,已知△ABC的三个顶点分别是格点A、B、C. 如图所示,圆周角有∠A、∠B、∠C、∠D.
如图所示,圆周角有∠A、∠B、∠C、∠D.