题目内容
如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?为什么?
考点:圆周角定理
专题:常规题型
分析:先画出几何图,AB和CD为⊙O的弦,且AB∥CD,连结BC,根据平行线的性质得∠ABC=∠BCD,根据圆周角定理得
=
,所以圆的两条弦互相平行,那么这两条弦所夹的弧相等.
 |
| AC |
 |
| BD |
解答: 解:如果圆的两条弦互相平行,那么这两条弦所夹的弧相等.理由如下:
解:如果圆的两条弦互相平行,那么这两条弦所夹的弧相等.理由如下:
如图,AB和CD为⊙O的弦,且AB∥CD,
连结BC,
∵AB∥CD,
∴∠ABC=∠BCD,
∴
=
,
所以圆的两条弦互相平行,那么这两条弦所夹的弧相等.
 解:如果圆的两条弦互相平行,那么这两条弦所夹的弧相等.理由如下:
解:如果圆的两条弦互相平行,那么这两条弦所夹的弧相等.理由如下:如图,AB和CD为⊙O的弦,且AB∥CD,
连结BC,
∵AB∥CD,
∴∠ABC=∠BCD,
∴
 |
| AC |
 |
| BD |
所以圆的两条弦互相平行,那么这两条弦所夹的弧相等.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
2013年我市财政收入达500亿元人民币,用科学记数法表示500亿元为( )
| A、5×1010元 |
| B、0.5×1010元 |
| C、5×1011元 |
| D、0.5×1012元 |
已知OC是∠AOB的平分线,则下列结论不正确的是( )
| A、∠AOC=∠BOC | ||
B、∠AOC=
| ||
| C、∠AOB=2∠BOC | ||
| D、∠AOB=∠BOC |
已知α为锐角,且cosα≤sin30°,则( )
| A、0°≤α≤60° |
| B、60°≤α<90° |
| C、0°<α≤30° |
| D、30°≤α<90° |
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=6,求BC和AB的长.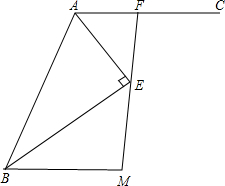 如图,AE平分∠BAC,BE⊥AE,AC∥BM,若AB=5,BM=4,求AF的长.
如图,AE平分∠BAC,BE⊥AE,AC∥BM,若AB=5,BM=4,求AF的长.