题目内容
3.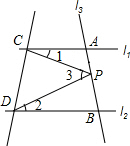 如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.(PC与l1所夹的角为∠1,PD与l2所夹的角为∠2,∠CPD为∠3)
如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.(PC与l1所夹的角为∠1,PD与l2所夹的角为∠2,∠CPD为∠3)(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)当点P在A、B两点间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系.(点P和A、B不重合,只要写出结论即可)
分析 (1)作PE∥AC,如图1,由于l1∥l2,则PE∥BD,根据平行线的性质得∠1=∠EPC,∠2=∠EPD,所以∠1+∠2=∠3;
(2)∠1、∠2、∠3之间的关系不发生变化,它们的关系为∠1+∠2=∠3;
(3)与(1)的证明方法一样可得∠1-∠2=∠3或∠2-∠1=∠3.
解答 解:(1)∠1+∠2=∠3.理由如下:
作PE∥AC,如图1,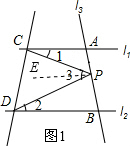
∵l1∥l2,
∴PE∥BD,
∴∠1=∠EPC,∠2=∠EPD,
∴∠1+∠2=∠3;
(2)∠1、∠2、∠3之间的关系不发生变化;
(3)∠1-∠2=∠3或∠2-∠1=∠3.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
14.将点A(3,-1)先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
| A. | (6,1) | B. | (0,-3) | C. | (0,1) | D. | (6,-3) |
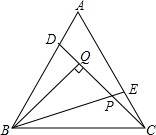 如图,点D,E分别是等边△ABC的两边AB,AC上的点,且AD=CE,BQ⊥CD于点Q,PQ=1,求BQ的长.
如图,点D,E分别是等边△ABC的两边AB,AC上的点,且AD=CE,BQ⊥CD于点Q,PQ=1,求BQ的长. 请采用两种不同的方法,在如图的方格纸中画出两条互相垂直的直线.
请采用两种不同的方法,在如图的方格纸中画出两条互相垂直的直线.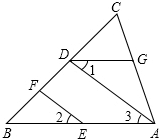 如图,EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
如图,EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.