题目内容
18.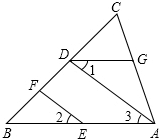 如图,EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
如图,EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.解:∵EF∥AD (已知)
∴∠2=∠3 (两直线平行同位角相等)
又∵∠1=∠2 (已知)
∴∠1=∠3 (等量代换)
∴AB∥DG (内错角相等两直线平行)
∴∠BAC+∠AGD=180°(两直线平行同旁内角互补)
∵∠BAC=75°(已知)
∴∠AGD=105°.
分析 先根据两直线平行同位角相等可得∠2=∠3,然后根据等量代换可得∠1=∠3,然后根据内错角相等两直线平行可得AB∥DG,然后根据两直线平行同旁内角互补可得∠BAC+∠AGD=180°,进而可求∠AGD的度数.
解答 解:∵EF∥AD (已知)
∴∠2=∠3 (两直线平行同位角相等)
又∵∠1=∠2 (已知)∴∠1=∠3 (等量代换)
∴AB∥DG (内错角相等两直线平行)
∴∠BAC+∠AGD=180°(两直线平行同旁内角互补)
∵∠BAC=75°(已知)
∴∠AGD=105°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;105°.
点评 此题考查了平行线的判定与性质,解题的关键是:熟记同位角相等?两直线平行;内错角相等?两直线平行;同旁内角互补?两直线平行.

练习册系列答案
相关题目
9.在下列函数中表示关于x的反比例函数的是( )
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=$\frac{2}{x+1}$ | D. | y=$\frac{2}{{x}^{2}}$ |
7.若点P(x,y)在第一象限,则点Q(x+y,x-y)一定不在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第二、三象限 | D. | 第二、四象限 |
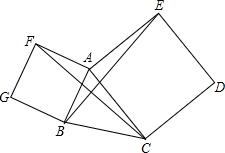 已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.
已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.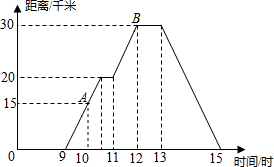 小明家在下白石,他很想一个人去穆阳白云山玩,不过他要先到赛岐停留下,然后在接着去穆阳白云山,他把一天的时间做了一个规划,下面是小明一天从0点到15点的离家距离的情况.
小明家在下白石,他很想一个人去穆阳白云山玩,不过他要先到赛岐停留下,然后在接着去穆阳白云山,他把一天的时间做了一个规划,下面是小明一天从0点到15点的离家距离的情况.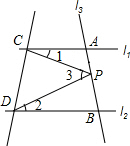 如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.(PC与l1所夹的角为∠1,PD与l2所夹的角为∠2,∠CPD为∠3)
如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.(PC与l1所夹的角为∠1,PD与l2所夹的角为∠2,∠CPD为∠3)