题目内容
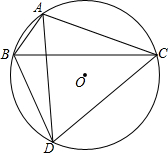 如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.
如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.①BC与BD满足什么数量关系?写出结论,并证明.
②AB,AC,AD之间满足什么数量关系?写出结论,并说明.
(最后一问要选择不同证明方法证明).
考点:圆周角定理,全等三角形的判定与性质
专题:
分析:(1)证明∠BDC=∠BCD=60°,即可解决问题.
(2)法①,如图,作辅助线,证明△ABC≌△MDC,得到AB=MD,即可解决问题;
法②,运用与法①类似的方法,即可解决问题.
(2)法①,如图,作辅助线,证明△ABC≌△MDC,得到AB=MD,即可解决问题;
法②,运用与法①类似的方法,即可解决问题.
解答:解:(1)BC=BD;证明如下:
∵∠BAC=120°,∠BAC+∠BDC=180°,
∴∠BDC=60°;
∵AD平分∠BAC,
∴∠BAD=∠CAD=60°,
∴∠BCD=∠BAD=60°,
∴∠BDC=∠BCD=60°,
∴BD=BC.
(2)法①,如图,在AD上截取AM=AC,连接MC;
∵∠MAC=60°,
∴△AMC是等边三角形,
∴∠AMC=60°,MC=AC;
∴∠DMC=120°;
在△ABC与△MDC中,
,
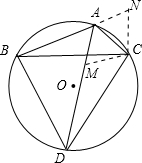 ∴△ABC≌△MDC(AAS),
∴△ABC≌△MDC(AAS),
∴AB=MD,AB+AC=DM+AM,
即AB+AC=AD.
法②,如图,延长BA到N,使AN=AC,连接NC;
类比法①,同理可证△ADC≌△NBC,
BN=AD,而BN=AB+AN=AB+AC,
即AB+AC=AD.
∵∠BAC=120°,∠BAC+∠BDC=180°,
∴∠BDC=60°;
∵AD平分∠BAC,
∴∠BAD=∠CAD=60°,
∴∠BCD=∠BAD=60°,
∴∠BDC=∠BCD=60°,
∴BD=BC.
(2)法①,如图,在AD上截取AM=AC,连接MC;
∵∠MAC=60°,
∴△AMC是等边三角形,
∴∠AMC=60°,MC=AC;
∴∠DMC=120°;
在△ABC与△MDC中,
|
 ∴△ABC≌△MDC(AAS),
∴△ABC≌△MDC(AAS),∴AB=MD,AB+AC=DM+AM,
即AB+AC=AD.
法②,如图,延长BA到N,使AN=AC,连接NC;
类比法①,同理可证△ADC≌△NBC,
BN=AD,而BN=AB+AN=AB+AC,
即AB+AC=AD.
点评:该题主要考查了圆周角定理、全等三角形的判定及其性质等几何知识点的应用问题;灵活运用有关定理来分析、判断、推理或解答是解题的关键.

练习册系列答案
相关题目
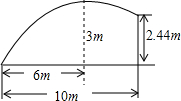 如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门?
如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门?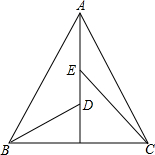 △ABC是等边三角形,∠ADB=120°,∠AEC=120°,求证:CE=BD+ED.
△ABC是等边三角形,∠ADB=120°,∠AEC=120°,求证:CE=BD+ED.