题目内容
某乒乓球俱乐部有10块训练场地对外出租,当每块场地每小时租金10元时,场地可全部租出;若每块场地每小时租金提高2元,则会减少1块场地租出;同时租出去的每块场地每小时需要支付各种费用2元,设每块场地每小时租金提高x(元),乒乓球俱乐部每小时的利润为y(元).
(1)求出y(元)与x(元)的函数关系式;
(2)每块场地每小时租金提高多少时,乒乓球俱乐部每小时的利润最大?最大利润是多少?
(1)求出y(元)与x(元)的函数关系式;
(2)每块场地每小时租金提高多少时,乒乓球俱乐部每小时的利润最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)利用总利润=每块场地的利润×块数列出函数关系式即可;
(2)利用配方法或公式法求得二次函数的最值即可.
(2)利用配方法或公式法求得二次函数的最值即可.
解答:解:(1)y=(10+x-2)(10-
)=-
x2+6x+80;
(3)∵y=-
x2+6x+80=-
(x-6)2+98,
∴每块场地每小时租金提高6元时,乒乓球俱乐部每小时的利润最大,最大利润是98元.
| x |
| 2 |
| 1 |
| 2 |
(3)∵y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴每块场地每小时租金提高6元时,乒乓球俱乐部每小时的利润最大,最大利润是98元.
点评:本题考查了二次函数的应用,解题的关键是从实际问题中整理出函数模型,并用函数的知识解决实际问题.

练习册系列答案
相关题目
 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和D(5,0).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和D(5,0).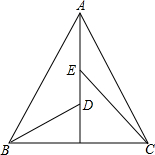 △ABC是等边三角形,∠ADB=120°,∠AEC=120°,求证:CE=BD+ED.
△ABC是等边三角形,∠ADB=120°,∠AEC=120°,求证:CE=BD+ED. 如图,D、B、C三点在同一直线上,∠C=50°,∠FBC=80°,问∠DBF的平分线BE与AC有怎样的位置关系?并说明理由.
如图,D、B、C三点在同一直线上,∠C=50°,∠FBC=80°,问∠DBF的平分线BE与AC有怎样的位置关系?并说明理由.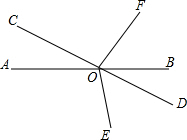 如图,直线AB、CD相交于点O,∠EOD=∠BOF,∠AOE与∠COF相等吗?为什么?
如图,直线AB、CD相交于点O,∠EOD=∠BOF,∠AOE与∠COF相等吗?为什么? 如图所示,已知△ABC内接于⊙O,过点A作直线EF切于⊙O,若∠B=50°,求∠CAE的度数.
如图所示,已知△ABC内接于⊙O,过点A作直线EF切于⊙O,若∠B=50°,求∠CAE的度数.