题目内容
11.计算:(1)($\frac{\sqrt{5}+1}{2}$)2-($\frac{\sqrt{5}-1}{2}$)2;
(2)($\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$)2+($\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)2(b2-4ac≥0,a≠0)
分析 (1)先利用平方差公式得到原式=($\frac{\sqrt{5}+1}{2}$-$\frac{\sqrt{5}-1}{2}$)($\frac{\sqrt{5}+1}{2}$+$\frac{\sqrt{5}-1}{2}$),然后把括号内合并后进行乘法运算;
(2)先利用完全平方公式计算,然后合并即可.
解答 解:(1)原式=($\frac{\sqrt{5}+1}{2}$-$\frac{\sqrt{5}-1}{2}$)($\frac{\sqrt{5}+1}{2}$+$\frac{\sqrt{5}-1}{2}$)
=1×$\sqrt{5}$
=$\sqrt{5}$;
(2)原式=$\frac{{b}^{2}+2b\sqrt{{b}^{2}-4ac}+{b}^{2}-4ac}{4{a}^{2}}$+$\frac{{b}^{2}-2b\sqrt{{b}^{2}-4ac}+{b}^{2}-4ac}{4{a}^{2}}$
=$\frac{4{b}^{2}-8ac}{4{a}^{2}}$
=$\frac{{b}^{2}-2ac}{{a}^{2}}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
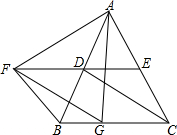 如图,点G在边BC上,△ABC和△AGF都是等边三角形,点E在边AC上,FE∥BC,EF和AB交于点D.
如图,点G在边BC上,△ABC和△AGF都是等边三角形,点E在边AC上,FE∥BC,EF和AB交于点D.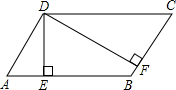 如图,在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若ABCD的周长为45,DE=5,DF=10,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若ABCD的周长为45,DE=5,DF=10,求平行四边形ABCD的面积.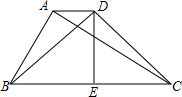 如图,梯形两条对角线BD,AC长分别为13和20,梯形的高为12,求梯形的面积.
如图,梯形两条对角线BD,AC长分别为13和20,梯形的高为12,求梯形的面积.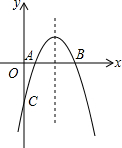 已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0)
已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0)