题目内容
16.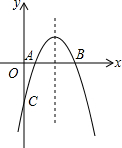 已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0)
已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0)(1)求抛物线的表达式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标.
分析 (1)由于已知抛物线与x轴的交点坐标,则可利用交点式求出抛物线解析式;
(2)根据二次函数图象上点的坐标特征,可设P(t,-t2+4t-3),根据三角形面积公式得到$\frac{1}{2}$•2•|-t2+4t-3|=1,然后去绝对值得到两个一元二次方程,再解方程求出t即可得到P点坐标.
解答 解:(1)抛物线解析式为y=-(x-1)(x-3)=-x2+4x-3;
(2)设P(t,-t2+4t-3),
因为S△PAB=1,AB=3-1=2,
所以$\frac{1}{2}$•2•|-t2+4t-3|=1,
当-t2+4t-3=1时,t1=t2=2,此时P点坐标为(2,1);
当-t2+4t-3=-1时,t1=2+$\sqrt{2}$,t2=2-$\sqrt{2}$,此时P点坐标为(2+$\sqrt{2}$,-1)或(2-$\sqrt{2}$,-1),
所以满足条件的P点坐标有3个,它们是(2,1)或(2+$\sqrt{2}$,-1)或(2-$\sqrt{2}$,-1).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
5.甲,乙,丙三位先生是同一家公司的职员,他们的夫人,M,N,P也都是这家公司的职员,知情者介绍说:“M的丈夫是乙的好友,并在三位先生中最年轻;丙的年龄比P的丈夫大”.根据该知情者提供的信息,我们可以推出三对夫妇分别是( )
| A. | 甲-M,乙-N,丙-P | B. | 甲-M,乙-P,丙-N | C. | 甲-N,乙-P,丙-M | D. | 甲-P,乙-N,丙-M |
 如图所示,△A′B′C′是△ABC经过平移后得到的A(-4,-1),B(-5,-4),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图所示,△A′B′C′是△ABC经过平移后得到的A(-4,-1),B(-5,-4),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).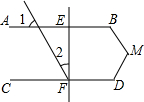 如图,EF为直线,∠1=63°,∠2=27°,且∠B+∠BMD+∠D=360°,EF垂直于CD吗?请证明你的结论.
如图,EF为直线,∠1=63°,∠2=27°,且∠B+∠BMD+∠D=360°,EF垂直于CD吗?请证明你的结论.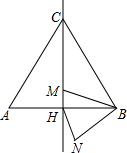 如图,边长为5的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是1.25.
如图,边长为5的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是1.25.