题目内容
9．现有长度分别为3cm和5cm的木棒，用5根长度为1cm、3cm、5cm、7cm、9cm的木棒分别与之围成三角形，则能围成三角形的概率为$\frac{3}{5}$．分析 根据三角形的三边关系得出第三根木棒的长度的取值范围，再根据概率公式即可得出答案．
解答 解：∵两根木棒的长分别是3cm和5cm，
∴第三根木棒的长度大于2cm，小于8cm，
∴能围成三角形的是：3cm、5cm、7cm的木棒，
∴能围成三角形的概率为$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．
点评 此题考查了列举法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图所示，P为△ABC内一点，∠BPC=150°，∠ABP=20°，∠ACP=30°，求∠A的度数．
20．下列式子中，属于最简二次根式的是（ ）
| A． | $\sqrt{6}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{8}$ | D． | $\sqrt{27}$ |
17．⊙O1与⊙O2的半径分别是6和4，若O1O2=3，则⊙O1与⊙O2的位置关系是（ ）
| A． | 相交 | B． | 相离 | C． | 内切 | D． | 外切 |
4．
要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，且有OA=OB=OC=OD，如果圆形工件恰好通过卡钳AB，则此工件的外径必是CD之长了，其中的依据是全等三角形的判定条件（ ）
要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，且有OA=OB=OC=OD，如果圆形工件恰好通过卡钳AB，则此工件的外径必是CD之长了，其中的依据是全等三角形的判定条件（ ）| A． | SSS | B． | SAS | C． | ASA | D． | AAS |
14．已知∠A=30°，则这个角的余角是（ ）
| A． | 30° | B． | 60° | C． | 90° | D． | 150° |
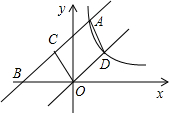如图，直线y=x+3交反比例函数y=-$\frac{k}{x}$的图象于点A，交x轴于点B，且过点C（-1，2），将直线AB向下平移，线段CA平移到线段OD，当点D也在反比例函数y=-$\frac{k}{x}$的图象上时，则k=-4．