题目内容
17.解不等式组$\left\{\begin{array}{l}{-\frac{1}{2}x≤2-x}\\{5x-1>3x-4}\end{array}\right.$,并求其整数解的和.分析 先分别解两不等式得到x≤4和x>-$\frac{3}{2}$,再利用大小小大中间找确定不等式组的解集,然后在x的取值范围内找出所有整数后计算它们的和即可.
解答 解:$\left\{\begin{array}{l}{-\frac{1}{2}x≤2-x①}\\{5x-1>3x-4②}\end{array}\right.$,
解①得x≤4,
解②得x>-$\frac{3}{2}$,
所以不等式组的解集为-$\frac{3}{2}$<x≤4,
所以不等式组的整数解为-1,0,1,2,3,4,
则所以整数解的和为-1+0+1+2+3+4=9.
点评 本题考查了解一元一次不等式组:求不等式组的解集的过程叫解不等式组.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
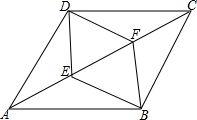 如图,?ABCD中,点E、F为对角线AC的三等分点,顺次连接点B、E、D、F.
如图,?ABCD中,点E、F为对角线AC的三等分点,顺次连接点B、E、D、F.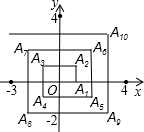 如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…则点A2013的坐标为(504,-503).
如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…则点A2013的坐标为(504,-503). 如图,∠D=30°,∠O=50°,∠C=35°,则∠AEC等于65°.
如图,∠D=30°,∠O=50°,∠C=35°,则∠AEC等于65°.