题目内容
1.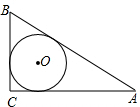 如图,Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r=1.
如图,Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r=1.
分析 首先求出AB的长,再连圆心和各切点,利用切线长定理用半径表示AF和BF,而它们的和等于AB,得到关于r的方程,即可求出.
解答 解:如图,设△ABC的内切圆与各边相切于D,E,F,连接OD,OE,OF,
则OE⊥BC,OF⊥AB,OD⊥AC,
设半径为r,CD=r,
∵∠C=90°,AC=4,BC=3,
∴AB=5,
∴BE=BF=3-r,AF=AD=4-r,
∴4-r+3-r=5,
∴r=1.
∴△ABC的内切圆的半径为 1.
故答案为;1.
点评 此题主要考查了勾股定理以及直角三角形内切圆半径求法等知识,熟练掌握切线长定理和勾股定理是解题的关键.

练习册系列答案
相关题目
12.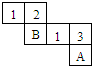 已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )
已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )
 已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )
已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )| A. | $\frac{1}{3}$,$\frac{1}{2}$ | B. | $\frac{1}{3}$,1 | C. | $\frac{1}{2}$,$\frac{1}{3}$ | D. | 1,$\frac{1}{3}$ |
6.下列图形中不是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
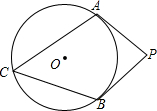 如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度.
如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度.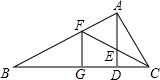 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ACB的平分线交AD于点E,交AB于点F,FG⊥BC于点G.求证:AE=FG.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ACB的平分线交AD于点E,交AB于点F,FG⊥BC于点G.求证:AE=FG. 如图,已知线段AB
如图,已知线段AB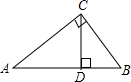 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.