题目内容
16.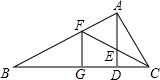 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ACB的平分线交AD于点E,交AB于点F,FG⊥BC于点G.求证:AE=FG.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ACB的平分线交AD于点E,交AB于点F,FG⊥BC于点G.求证:AE=FG.
分析 根据角平分线上的点到两边的距离相等可得:FG=FA;则只要在确定FA与AE的关系即可确定AE与FG之间的关系;在直角三角形AFC中∠AFC+∠ACF=90°,在直角三角形CDE中,∠DEC+∠ECD=90°,根据角平分线的性质可知:∠ACF=∠DCE,则∠AFC=∠DEC,又知∠AEF=∠DEC,则∠AFC=∠AEF,所以AE=FA,则AE=FG.
解答 证明:∵CF平分∠ACB,FA⊥AC,FG⊥BC
∴FG=FA
∵∠AFC+∠ACF=90°,∠DEC+∠ECD=90°,且∠ACF=∠ECD
∴∠AFC=∠DEC
∵∠AEF=∠DEC
∴∠AFC=∠AEF
∴AE=FA
∴AE=FG.
点评 本题主要考查了等腰三角形的判定和性质,角平分线的性质;解题时利用了AF这个中间量进行了等量代换是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列四个几何体中,左视图与其它三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
4.若分式方程$\frac{x}{x+2}=\frac{m}{x+2}$无解,则m的值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
11.下列长度的线段能组成一个三角形的是( )
| A. | 15cm、10cm、7cm | B. | 4cm、5cm、10cm | C. | 3cm、8cm、5cm | D. | 3cm、3cm、6cm |
5.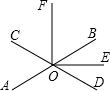 如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )
如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )
 如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )
如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )| A. | 50° | B. | 75° | C. | 65° | D. | 55° |
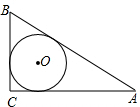 如图,Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r=1.
如图,Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r=1.