题目内容
10. 如图,点A的坐标为(3,2),点B的坐标为(3,0).作如下操作:
如图,点A的坐标为(3,2),点B的坐标为(3,0).作如下操作:①以点A为旋转中心,将△ABO顺时针方向旋转90°,得到△AB1O1;
②以点O为位似中心,将△ABO放大,得到△A2B2O,使位似比为1:2,且点A2在第三象限.
(1)在图中画出△AB1O1和△A2B2O;
(2)请直接写出点A2的坐标:(-6,-4).
(3)如果△ABO内部一点M的坐标为(m,n),写出点M在△A2B2O内的对应点N的坐标:(-2m,-2n).
分析 (1)根据旋转变换的条件以及位似变换的条件作出图形即可.
(2)根据图象即可写出点A2坐标.
(3)根据位似变换,点A的变化规律,得出位似变换的点的变化规律,即可解决问题.
解答 解:(1)△AB1O1和△A2B2O,如图所示,
(2)由图象可知,A2(-6,-4).
故答案为(-6,-4).
(3)△ABO内部一点M的坐标为(m,n),点M在△A2B2O内的对应点N的坐标为(-2m,-2n).
故答案为(-2m,-2n).
点评 本题考查作图-位似变换、作图-旋转变换等知识,解题的关键是熟练掌握作旋转变换图形,作位似变换的图形,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知反比例函数y=$\frac{k}{x}$(k≠0)的图象在其所在现象内,y的值随x的值的增大而增大,则反比例函数y=$\frac{k}{x}$的图象在( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
2.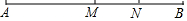 如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )
如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )
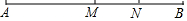 如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )
如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.下列是一元一次方程的是( )
| A. | $\frac{2}{x}$-3=0 | B. | x+5y=4 | C. | 2x+3 | D. | 5x+3=4 |
 如图是由5个大小相同的小立方体组成的立体图形,这个立体图形的俯视图是( )
如图是由5个大小相同的小立方体组成的立体图形,这个立体图形的俯视图是( )


