题目内容
2．一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为8．分析 首先设第三边长为x，根据三角形的三边关系可得3-2＜x＜3+2，然后再确定x的值，进而可得周长．
解答 解：设第三边长为x，
∵两边长分别是2和3，
∴3-2＜x＜3+2，
即：1＜x＜5，
∵第三边长为奇数，
∴x=3，
∴这个三角形的周长为2+3+3=8，
故答案为：8．
点评 此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边，三角形的两边差小于第三边．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
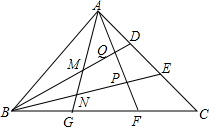△ABC面积为S，AD=DE=EC，BG=GF=FC，AG，AF与BD，BE分别交于M，N，P，Q，连接EF．
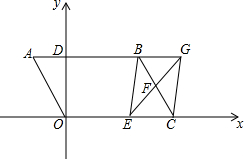如图，平行四边形OABC中，OA=2$\sqrt{3}$，∠A=60°，AB交y轴于点D，点C（3$\sqrt{3}$，0），F是BC的中点，E在OC上从O向C移动，EF的延长线与AB的延长线交于点G．
17．下列计算正确的是（ ）
| A． | 3x2•2x=6x3 | B． | x6÷x3=x2 | C． | （3a）2=3a2 | D． | （a+b）2=a2+b2 |
7．-3的绝对值是（ ）
| A． | 3 | B． | -$\frac{1}{3}$ | C． | -3 | D． | $\frac{1}{3}$ |
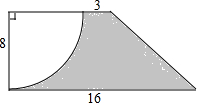求图中阴影部分的面积（单位：分米）．