题目内容
15.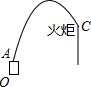 如图是某运动会开幕式点燃火炬的示意图,发射台OA的高度为2m,火炬的高度为12m,距发射台OA的水平距离为20m,在A处的发射装置向目标C发射一个火球点燃火炬,该火球运动的轨迹为抛物线形,当火球运动到距离地面最大高度20m时,相应的水平距离为12m,请你判断该火球能否点燃目标C?并说明理由.
如图是某运动会开幕式点燃火炬的示意图,发射台OA的高度为2m,火炬的高度为12m,距发射台OA的水平距离为20m,在A处的发射装置向目标C发射一个火球点燃火炬,该火球运动的轨迹为抛物线形,当火球运动到距离地面最大高度20m时,相应的水平距离为12m,请你判断该火球能否点燃目标C?并说明理由.
分析 由已知得抛物线的顶点及经过一点,可设抛物线解析式的顶点式.确定C点坐标,代入解析式即可作出判断.
解答 解:能,
由题意可知抛物线的顶点B坐标为(12,20)可设火球运行抛物线解析式为:
y=a(x-12)2+20,
把点A(0,2)代入解析式得:2=a(0-12)2+20,
解得:a=-$\frac{1}{8}$,
∴火球运行轨迹的抛物线对应的函数解析式为:
y=-$\frac{1}{8}$(x-12)2+20=-$\frac{1}{8}$x2+3x+2;
∵点C坐标为:(20,12),
代入y=-$\frac{1}{8}$x2+3x+2,左右相等,
所以点C在抛物线上,故能点燃目标.
点评 本题考查了实际问题中确定点的坐标及二次函数的实际应用.旨在培养学生数学建模思想,借助二次函数解决实际问题.

练习册系列答案
相关题目
6.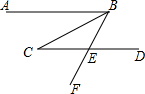 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )| A. | 16° | B. | 33° | C. | 49° | D. | 66° |
3.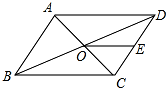 如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
 如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
如图,平行四边形ABCD的周长为36,对角线AC、BD相较于点O,点E是CD的中点,BD=12,则△DOE的周长为( )| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
20.已知两点A(5,6)、B(7,2),先将线段AB向左平移一个单位,再以原点O为位似中心,在第一象限内将其缩小为原来的$\frac{1}{2}$得到线段CD,则点A的对应点C的坐标为( )
| A. | (2,3) | B. | (3,1) | C. | (2,1) | D. | (3,3) |
7.-3的绝对值是( )
| A. | 3 | B. | -$\frac{1}{3}$ | C. | -3 | D. | $\frac{1}{3}$ |
4.某商品经过连续两次降价,销售单价由原来200元降到162元.设平均每次降价的百分率为x,根据题意可列方程为( )
| A. | 200(1-x)2=162 | B. | 200(1+x)2=162 | C. | 162(1+x)2=200 | D. | 162(1-x)2=200 |
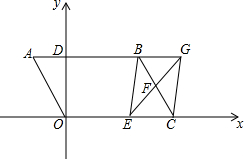 如图,平行四边形OABC中,OA=2$\sqrt{3}$,∠A=60°,AB交y轴于点D,点C(3$\sqrt{3}$,0),F是BC的中点,E在OC上从O向C移动,EF的延长线与AB的延长线交于点G.
如图,平行四边形OABC中,OA=2$\sqrt{3}$,∠A=60°,AB交y轴于点D,点C(3$\sqrt{3}$,0),F是BC的中点,E在OC上从O向C移动,EF的延长线与AB的延长线交于点G.