题目内容
14．若直线y=m-1（m为常数）与函数y=$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}（x≤2）}\\{\frac{4}{x}（x＞2）}\end{array}\right.$的图象恒有三个不同的交点，则常数m的取值范围是1＜m＜3．分析 根据已知解析式画出函数图象，进而得出常数m的取值范围．
解答 
解：如图所示：当x=2时，y=2，
故直线y=m-1（m为常数）与函数y=$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}（x≤2）}\\{\frac{4}{x}（x＞2）}\end{array}\right.$的图象恒有三个不同的交点，
则常数m的取值范围是：1＜m＜3．
故答案为：1＜m＜3．
点评 此题主要考查了二次函数与反比例函数的图象，利用数形结合得出m的取值范围是解题关键．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
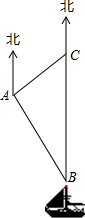南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，当渔船航行至海面B处时，测得该岛位于正北方向25海里的C处，为了防止某国海巡警干扰，就请求我A处的渔监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西33°的方向上，求A，C之间的距离．（参考数据：sin33°≈0.545，cos33°≈0.839，tan33°≈0.649，$\sqrt{2}$≈1.414，结果保留一位小数）
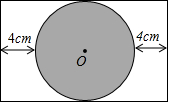电视显示屏的屏保图是阴影部分的圆O（矩形中最大的圆），屏保图在显示屏（矩形）中的位置如图，若⊙O的面积为400πcm2，求矩形显示屏的长．
9．下列各式的变形中，正确的是（ ）
| A． | x6÷x=x | B． | （x2-$\frac{1}{x}$）÷x=x-1 | C． | x2+x3=x5 | D． | x2-x+1=（x-$\frac{1}{2}$）2+$\frac{3}{4}$ |
实数a、b在数轴上对应的如图所示，化简$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{（{a-b}）}^2}}$=-2a．