题目内容
13.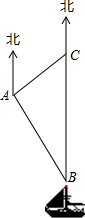 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至海面B处时,测得该岛位于正北方向25海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西33°的方向上,求A,C之间的距离.(参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649,$\sqrt{2}$≈1.414,结果保留一位小数)
南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至海面B处时,测得该岛位于正北方向25海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西33°的方向上,求A,C之间的距离.(参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649,$\sqrt{2}$≈1.414,结果保留一位小数)
分析 作AD⊥BC,垂足为D,设CD=x,利用解直角三角形的知识,可得出AD,继而可得出BD,结合题意BC=CD+BD可得出方程,解出x的值后即可得出答案.
解答  解:如图,作AD⊥BC,垂足为D,
解:如图,作AD⊥BC,垂足为D,
由题意得,∠ACD=45°,∠ABD=33°.
设CD=x,在Rt△ACD中,可得AD=x,
在Rt△ABD中,可得BD=cot33°x,
又∵BC=25海里,CD+BD=BC,
即x+cot33°x=25,
所以x+$\frac{0.839}{0.545}$x=25
解得:x≈14.5,
∴AC=$\sqrt{2}$ x=20.5 (海里).
答:A、C之间的距离为20.5 海里.
点评 此题考查了解直角三角形的应用,解答本题的关键是根据题意构造直角三角形,将实际问题转化为数学模型进行求解,难度一般.

练习册系列答案
相关题目
18.下列选项中,不适合抽样调查而适合普查的是( )
| A. | 了解某路口每天在学校放学时段的车流量 | |
| B. | 检测某种新型LED灯的使用寿命 | |
| C. | 检测站对本市所有公交车的年度安全检查 | |
| D. | 了解同一批青菜的农药残留量 |
2.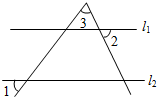 如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )
如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )
 如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )
如图,直线l1∥l2,∠1=55°,∠3=65°,则∠2大小为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
 已知A(0,8),B(6,0),在坐标轴上取一点P,使三角形ABP为等腰三角形,求P点的坐标.
已知A(0,8),B(6,0),在坐标轴上取一点P,使三角形ABP为等腰三角形,求P点的坐标. 乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).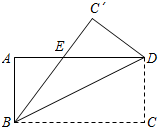 把矩形ABCD沿着对角线BD折叠,使点C落在C′处,交AD于E,若AD=8,AB=4,则AE的长为( )
把矩形ABCD沿着对角线BD折叠,使点C落在C′处,交AD于E,若AD=8,AB=4,则AE的长为( ) 如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.