题目内容
19. 如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过4029或4030次移动后该点到原点的距离为2015个单位长度.
如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过4029或4030次移动后该点到原点的距离为2015个单位长度.
分析 根据数轴上点的坐标变化和平移规律(左减右加),分别求出点所对应的数,进而求出点到原点的距离;然后对奇数项、偶数项分别探究,找出其中的规律(相邻两数都相差3),写出表达式就可解决问题.
解答 解:第1次点A向右移动1个单位长度至点B,则B表示的数,0+1=1;
第2次从点B向左移动2个单位长度至点C,则C表示的数为1-2=-1;
第3次从点C向右移动3个单位长度至点D,则D表示的数为-1+3=2;
第4次从点D向左移动4个单位长度至点E,则点E表示的数为2-4=-2;
第5次从点E向右移动5个单位长度至点F,则F表示的数为-2+5=3;
…;
由以上数据可知,当移动次数为奇数时,点在数轴上所表示的数满足:$\frac{1}{2}$(n+1),
当移动次数为偶数时,点在数轴上所表示的数满足:-$\frac{1}{2}$n,
当移动次数为奇数时,$\frac{1}{2}$(n+1)=2015,n=4029,
当移动次数为偶数时,-$\frac{1}{2}$n=-2015,n=4030.
故答案为:4029或4030.
点评 本题考查了数轴,以及用正负数可以表示具有相反意义的量,还考查了数轴上点的坐标变化和平移规律(左减右加),考查了一列数的规律探究.对这列数的奇数项、偶数项分别进行探究是解决这道题的关键.

练习册系列答案
相关题目
14.下列分式从左至右的变形正确的是( )
| A. | $\frac{-a}{2b}=\frac{a}{-2b}$ | B. | $\frac{1}{n}=\frac{m+1}{m+n}$ | C. | $\frac{{y}^{2}+y}{xy}=\frac{y+1}{xy}$ | D. | $\frac{a}{b}=\frac{a{c}^{2}}{b{c}^{2}}$ |
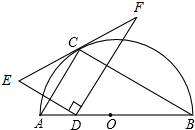 如图点C在以AB为直径的半圆的圆周上,若AB=4,∠ABC=30°,D为边AB上一动点,点E和D关于AC对称,当D与A重合时,F为EC的延长线上满足CF=EC的点,当D与A不重合时,F为EC的延长线与过D且垂直于DE的直线的交点,
如图点C在以AB为直径的半圆的圆周上,若AB=4,∠ABC=30°,D为边AB上一动点,点E和D关于AC对称,当D与A重合时,F为EC的延长线上满足CF=EC的点,当D与A不重合时,F为EC的延长线与过D且垂直于DE的直线的交点, 如图1,⊙O是等边三角形ABC的外接圆,P是⊙O上的一个点.
如图1,⊙O是等边三角形ABC的外接圆,P是⊙O上的一个点. 如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.