题目内容
12.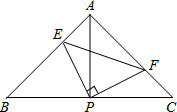 如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:
如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤2S四边形AEPF=S△ABC.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的序号有①②③⑤.
分析 根据等腰直角三角形的性质可得AP⊥BC,AP=PC,∠EAP=∠C=45°,根据同角的余角相等求出∠APE=∠CPF,判定②正确,然后利用“角边角”证明△APE和△CPF全等,根据全等三角形的可得AE=CF,判定①正确,再根据等腰直角三角形的定义得到△EFP是等腰直角三角形,判定③正确;根据等腰直角三角形的斜边等于直角边的$\sqrt{2}$倍表示出EF,可知EF随着点E的变化而变化,判定④错误;根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半,判定⑤正确.
解答 解:∵AB=AC,∠BAC=90°,点P是BC的中点,
∴AP⊥BC,AP=PC,∠EAP=∠C=45°,
∴∠APF+∠CPF=90°,
∵∠EPF是直角,
∴∠APF+∠APE=90°,
∴∠APE=∠CPF,故②正确;
在△APE和△CPF中,
$\left\{\begin{array}{l}{∠APE=∠CPF}\\{AP=PC}\\{∠EAP=∠C=4{5}^{°}}\end{array}\right.$,
∴△APE≌△CPF(ASA),
∴AE=CF,故①正确;
∴△EFP是等腰直角三角形,故③正确;
根据等腰直角三角形的性质,EF=$\sqrt{2}$PE,
所以,EF随着点E的变化而变化,只有当点E为AB的中点时,EF=$\sqrt{2}$PE=AP,在其它位置时EF≠AP,故④错误;
∵△APE≌△CPF,
∴S△APE=S△CPF,
∴S四边形AEPF=S△APF+S△APE=S△APF+S△CPF=${S}_{△APC}=\frac{1}{2}$=S△ABC,故⑤正确,
综上所述,正确的结论有①②③⑤共4个.
故答案为:①②③⑤.
点评 本题考查了旋转的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,根据同角的余角相等求出∠APE=∠CPF,从而得到△APE和△CPF全等是解题的关键,也是本题的突破点.

| A. | a3+a3=a6 | B. | (a3)2=a5 | C. | a2+a2=2a2 | D. | 6a÷a=5a |
 如图,a∥b,∠1=72°,则∠2的度数是( )
如图,a∥b,∠1=72°,则∠2的度数是( )| A. | 72° | B. | 80° | C. | 82° | D. | 108° |
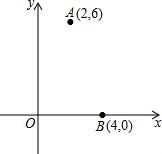 如图,在平面直角坐标系xOy中,已知定点A、B的坐标分别为(2,6),(4,0),在y轴上求一点C,使△ABC的周长最小,并求此时△ABC的面积.
如图,在平面直角坐标系xOy中,已知定点A、B的坐标分别为(2,6),(4,0),在y轴上求一点C,使△ABC的周长最小,并求此时△ABC的面积. 如图,菱形ABCD中,AE垂直平分BC,垂足为E,AB=2cm.那么菱形ABCD的对角线BD的长是$2\sqrt{3}$cm.
如图,菱形ABCD中,AE垂直平分BC,垂足为E,AB=2cm.那么菱形ABCD的对角线BD的长是$2\sqrt{3}$cm.