题目内容
3．
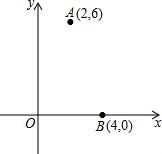如图，在平面直角坐标系xOy中，已知定点A、B的坐标分别为（2，6），（4，0），在y轴上求一点C，使△ABC的周长最小，并求此时△ABC的面积．
分析 作B关于y轴的对称点D，连接AD交y轴于C，此时DC=BC，则AC+BC=AC+DC=AD，根据两点之间线段最短可知此时△ABC的周长最小，设直线AD的解析式为y=kx+b，然后利用待定系数法即可求得b的值，从而求得C的坐标，然后根据S△ABC=S△ABD-S△BCD即可求得三角形ABC的面积．
解答 
解：作B关于y轴的对称点D，连接AD交y轴于C，此时DC=BC，则AC+BC=AC+DC=AD，根据两点之间线段最短可知此时△ABC的周长最小，
∵B（4，0），
∴D（-4，0），
∴BD=8，
设直线AD的解析式为y=kx+b，
∴$\left\{\begin{array}{l}{-4k+b=0}\\{2k+b=6}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=1}\\{b=4}\end{array}\right.$．
∴C（0，4），
∴S△ABC=S△ABD-S△BCD=$\frac{1}{2}$BD×6-$\frac{1}{2}$BD×4=$\frac{1}{2}$×8×2=8．
点评 本题考查了轴对称-最短路线问题，待定系数法求一次函数的解析式，三角形的面积等，确定C的位置是解题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
如图，在△ABC中AB=17，AC=10，BC边上的高AD=8，则边BC的长为21．
18．下列各式一定成立的是（ ）
| A． | $\sqrt{（a+b}{）^2}=a+b$ | B． | $\sqrt{{{（{a^2}+1）}^2}}={a^2}+1$ | C． | $\sqrt{（{a^2}-1）}={a^2}-1$ | D． | $\sqrt{{{（ab）}^2}}=ab$ |
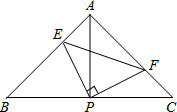如图：已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，给出以下五个结论：
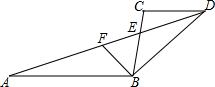如图，已知AB∥CD，AD与BC相交于点E，BF平分∠ABC交AD于F．