题目内容
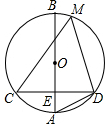 如图,⊙O的直径AB⊥CD于E,点M为⊙O上一点,tan∠CDA=
如图,⊙O的直径AB⊥CD于E,点M为⊙O上一点,tan∠CDA=| 1 |
| 2 |
(1)求证:BE=CD;
(2)若OE=3,求sin∠CMD.
考点:垂径定理,圆周角定理,解直角三角形
专题:
分析:(1)先根据垂径定理得出CD=2DE,再由tan∠CDA=
可知
=
,设AE=x,⊙O的半径等于r,则DE=2x,连接OD,在Rt△ODE中,OD=r,OE=r-x,根据勾股定理用x表示出r及OE的值,进而可得出结论;
(2)根据OE=3,即1.5x=3可得出x的值,故DE=4,BE=CD=8,AE=2,r=OD=5,再由∠CMD=∠EOD可得出结论.
| 1 |
| 2 |
| AE |
| DE |
| 1 |
| 2 |
(2)根据OE=3,即1.5x=3可得出x的值,故DE=4,BE=CD=8,AE=2,r=OD=5,再由∠CMD=∠EOD可得出结论.
解答: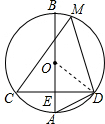 解:(1)∵⊙O的直径AB⊥CD于E,
解:(1)∵⊙O的直径AB⊥CD于E,
∴CD=2DE.
∵tan∠CDA=
∴
=
.
∴设AE=x,⊙O的半径等于,则DE=2x,
连接OD,在Rt△ODE中,OD=r,OE=r-x
由勾股定理得:(r-x)2+(2x)2=r2,
解得r=2.5x,OE=1.5x,
∴BE=2.5x+1.5x=4x,
∵CD=2DE=4x,
∴BE=CD;
(2)∵OE=3,即1.5x=3,
∴x=2,
∴DE=4,BE=CD=8,AE=2,r=OD=5,
∵∠CMD=∠EOD,
∴sin∠CMD=sin∠EOD=
=
.
 解:(1)∵⊙O的直径AB⊥CD于E,
解:(1)∵⊙O的直径AB⊥CD于E,∴CD=2DE.
∵tan∠CDA=
| 1 |
| 2 |
∴
| AE |
| DE |
| 1 |
| 2 |
∴设AE=x,⊙O的半径等于,则DE=2x,
连接OD,在Rt△ODE中,OD=r,OE=r-x
由勾股定理得:(r-x)2+(2x)2=r2,
解得r=2.5x,OE=1.5x,
∴BE=2.5x+1.5x=4x,
∵CD=2DE=4x,
∴BE=CD;
(2)∵OE=3,即1.5x=3,
∴x=2,
∴DE=4,BE=CD=8,AE=2,r=OD=5,
∵∠CMD=∠EOD,
∴sin∠CMD=sin∠EOD=
| DE |
| OD |
| 4 |
| 5 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 已知一个几何体的主视图和俯视图如图,请根据已知视图想象几何体的可能形状,并按照你的想象补画出两种不同的左视图.
已知一个几何体的主视图和俯视图如图,请根据已知视图想象几何体的可能形状,并按照你的想象补画出两种不同的左视图. 如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE=
如图,已知BD是∠ABC的角平分线,DE⊥AB于E点,AB=6cm,BC=4cm,S△ABC=10cm2,则DE= 如图,已知AB∥CD,直线EF分别截AB,CD于点M,N,MG、NH分别是∠EMB与∠END的平分线,试说明MG∥NH成立的理由.
如图,已知AB∥CD,直线EF分别截AB,CD于点M,N,MG、NH分别是∠EMB与∠END的平分线,试说明MG∥NH成立的理由.
 如图,∠1=∠2,∠3=100°,∠B=80°,那么DC∥EF,为什么?
如图,∠1=∠2,∠3=100°,∠B=80°,那么DC∥EF,为什么?