题目内容
求证:圆的内接四边形对角互补.
考点:圆内接四边形的性质
专题:证明题
分析:根据命题和题目提供的图形写出已知、求证、证明后,利用圆周角定理进行证明即可.
解答: 解:已知:四边形ABCD为⊙O的内接四边形,
解:已知:四边形ABCD为⊙O的内接四边形,
求证:∠B+∠D=180°,
证明:连接AO,CO,
由圆周角定理得:∠B=
∠1,∠D=
∠2,
∵∠1+∠2=360°,
∴∠B+∠D=180°
 解:已知:四边形ABCD为⊙O的内接四边形,
解:已知:四边形ABCD为⊙O的内接四边形,求证:∠B+∠D=180°,
证明:连接AO,CO,
由圆周角定理得:∠B=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠1+∠2=360°,
∴∠B+∠D=180°
点评:本题考查了圆内接四边形的性质及圆周角定理的知识,解题的关键是首先根据题意用数学语言将命题转化成符号语言.

练习册系列答案
相关题目
半径为5的圆中,72°圆心角所对弧长为( )
| A、π | B、2π | C、4π | D、5π |
 已知图中的两个三角形全等,则∠α度数是( )
已知图中的两个三角形全等,则∠α度数是( )| A、50° | B、58° |
| C、60° | D、72° |
下列计算正确的是( )
| A、(a3)2=a6 |
| B、a•a2=a2 |
| C、a3+a2=a6 |
| D、(3a)3=9a3 |
 如图,已知线段AB,请用尺规按下列要求作图.
如图,已知线段AB,请用尺规按下列要求作图. 如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=53°,则∠BOC的度数是
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=53°,则∠BOC的度数是
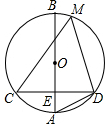 如图,⊙O的直径AB⊥CD于E,点M为⊙O上一点,tan∠CDA=
如图,⊙O的直径AB⊥CD于E,点M为⊙O上一点,tan∠CDA=