题目内容
 如图,已知AB∥CD,直线EF分别截AB,CD于点M,N,MG、NH分别是∠EMB与∠END的平分线,试说明MG∥NH成立的理由.
如图,已知AB∥CD,直线EF分别截AB,CD于点M,N,MG、NH分别是∠EMB与∠END的平分线,试说明MG∥NH成立的理由.考点:平行线的判定与性质
专题:
分析:由AB∥CD可得到∠EMB=∠MND,结合角平分线的定义可求得∠1=∠2,可判定MG∥NH.
解答:解:MG∥NH,理由如下:
∵AB∥CD,
∴∠EMB=∠MND,
又MG、NH分别是∠EMB与∠END的平分线,
∴∠EMB=2∠1,∠MND=2∠2,
∴∠1=∠2,
∴MG∥NH.
∵AB∥CD,
∴∠EMB=∠MND,
又MG、NH分别是∠EMB与∠END的平分线,
∴∠EMB=2∠1,∠MND=2∠2,
∴∠1=∠2,
∴MG∥NH.
点评:本题主要考查平行线的判定和性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
半径为5的圆中,72°圆心角所对弧长为( )
| A、π | B、2π | C、4π | D、5π |
 已知图中的两个三角形全等,则∠α度数是( )
已知图中的两个三角形全等,则∠α度数是( )| A、50° | B、58° |
| C、60° | D、72° |
若2m+n=-3,则4-4m-2n的值是( )
| A、-2 | B、10 | C、7 | D、1 |
 根据正弦函数的定义你能得出锐角正弦值的取值范围吗?
根据正弦函数的定义你能得出锐角正弦值的取值范围吗?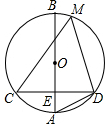 如图,⊙O的直径AB⊥CD于E,点M为⊙O上一点,tan∠CDA=
如图,⊙O的直径AB⊥CD于E,点M为⊙O上一点,tan∠CDA=