题目内容
10.解方程:(1)x2+4x-7=0
(2)5x(x-3)=(x+1)(x-3)
分析 (1)求出b2-4ac的值,再代入公式求出即可;
(2)移项,分解因式,再代入公式求出即可.
解答 解:(1)x2+4x-7=0,
△=42-4×1×(-7)=44,
x=$\frac{-4±\sqrt{44}}{2}$,
x1=-2+$\sqrt{11}$,x2=-2-$\sqrt{11}$;
(2)5x(x-3)=(x+1)(x-3),
5x(x-3)-(x+1)(x-3)=0,
(x-3)5x-x-1)=0,
x-3=0,5x-x-1=0,
x1=3,x2=$\frac{1}{4}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键,难度适中.

练习册系列答案
相关题目
18.已知甲、乙两组数据的平均数分别是${\overline x_甲}$=80,${\overline x_乙}$=90,方差分别是S甲2=10,S乙2=5,比较这两组数据,下列说法正确的是( )
| A. | 甲组数据较好 | B. | 乙组数据较好 | ||
| C. | 甲组数据比较整齐 | D. | 乙组数据的波动较小 |
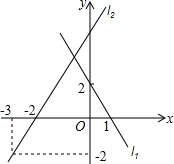 如图,直线l1、l2相交于点A,试求出点A的坐标.
如图,直线l1、l2相交于点A,试求出点A的坐标.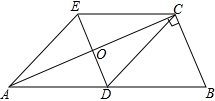 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.