题目内容
已知关于x的方程kx2+(k+2) x+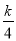 =0有两个不相等的实数根,则k的取值范围是__________.
=0有两个不相等的实数根,则k的取值范围是__________.
练习册系列答案
相关题目
7.已知四边形ABCD中,AC与BD交于点O,如果只给出条件“AB∥CD”,那么可以判定四边形ABCD是平行四边形的是( )
①再加上条件“BC=AD”,则四边形ABCD一定是平行四边形.
②再加上条件“∠BAD=∠BCD”,则四边形ABCD一定是平行四边形.
③再加上条件“AO=CO”,则四边形ABCD一定是平行四边形.
④再加上条件“∠DBA=∠CAB”,则四边形ABCD一定是平行四边形.
①再加上条件“BC=AD”,则四边形ABCD一定是平行四边形.
②再加上条件“∠BAD=∠BCD”,则四边形ABCD一定是平行四边形.
③再加上条件“AO=CO”,则四边形ABCD一定是平行四边形.
④再加上条件“∠DBA=∠CAB”,则四边形ABCD一定是平行四边形.
| A. | ①和② | B. | ①③和④ | C. | ②和③ | D. | ②③和④ |
8.-3是3的( )
| A. | 平方根 | B. | 倒数 | C. | 相反数 | D. | 绝对值 |
4. 如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )
如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )
 如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )
如图,已知直线AB∥CD,∠C=105°,∠A=45°,那么∠E的值为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
10.某学习小组,在探究1+$\frac{2}{x}$的性质时,得到了如下数据:
根据表格中的数据,做出了四个推测:
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| x | 1 | 10 | 100 | 1000 | 10000 | … |
| 1+$\frac{2}{x}$ | 3 | 1.2 | 1.02 | 1.002 | 1.0002 | … |
①1+$\frac{2}{x}$(x>0)的值随着x的增大而减小;
②1+$\frac{2}{x}$(x>0)的值有可能等于1;
③1+$\frac{2}{x}$(x>0)的值随着x的增大越来越接近于1;
④1+$\frac{2}{x}$(x>0)的值最大值是3.则推测正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列命题中是假命题的是( )
| A. | △ABC中,若∠A=∠C-∠B,则△ABC是直角三角形 | |
| B. | △ABC中,若a2=b2-c2,则△ABC是直角三角形 | |
| C. | △ABC中,若a:b:c=5:12:13,则△ABC是直角三角形 | |
| D. | △ABC中,若∠A,∠B,∠C的度数比是3:4:5,则△ABC是直角三角形 |


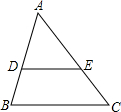 如图,已知$\frac{AD}{BD}$=$\frac{AE}{EC}$=$\frac{3}{2}$,试求$\frac{DE}{BC}$的值.
如图,已知$\frac{AD}{BD}$=$\frac{AE}{EC}$=$\frac{3}{2}$,试求$\frac{DE}{BC}$的值.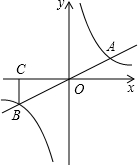 如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.
如图,正比例函数y=$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,过B作BC⊥x轴,垂足为C,且△BOC的面积等于4.