题目内容
14.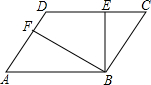 如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=60°,则?ABCD的周长为20.
如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=60°,则?ABCD的周长为20.
分析 由在?ABCD中,BE⊥CD,BF⊥AD,∠EBF=60°,可求得∠ABF=∠CBF=30°,然后由CE=2,DF=1,利用含30°的直角三角形的性质,即可求得答案.
解答 解:∵在?ABCD中,BE⊥CD,BF⊥AD,∠EBF=60°,
∴∠ABF=∠CBF=90°-∠EBF=30°,
∵在Rt△BCE中,CE=2,
∴BC=2CE=4,
∴AD=BC=4,
∵DF=1,
∴AF=AD-DF=3,
在Rt△ABF中,AB=2AF=6,
∴CD=AB=6,
∴?ABCD的周长为:2(AB+BC)=2×(4+6)=20.
故答案为:20.
点评 此题考查了平行四边形的性质以及含30°的直角三角形的性质.注意得到△ABF与△BCE是含30°的直角三角形是解此题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
5.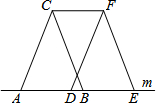 如图所示,三角形ABC沿直线m向右平移a厘米,得到三角形DEF,下列说法中错误的是( )
如图所示,三角形ABC沿直线m向右平移a厘米,得到三角形DEF,下列说法中错误的是( )
 如图所示,三角形ABC沿直线m向右平移a厘米,得到三角形DEF,下列说法中错误的是( )
如图所示,三角形ABC沿直线m向右平移a厘米,得到三角形DEF,下列说法中错误的是( )| A. | AC∥DF | B. | CF∥AB | C. | CF=a厘米 | D. | BD=a厘米 |
4.五张完全相同的卡片上,分别写上数字-3,-2,-1,2,3,现从中随机抽取一张,抽到写有负数的卡片的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
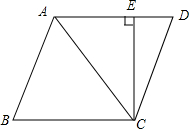 如图,AC是?ABCD的对角线,CE⊥AD,垂足为点E.
如图,AC是?ABCD的对角线,CE⊥AD,垂足为点E.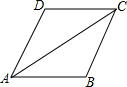 如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.