题目内容
19.已知点A(-1,y1),B (2,y2)是反比例函数y=-$\frac{5}{x}$的图象上的两点,下列结论正确的是( )| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
分析 先根据反比例函数的解析式判断出其函数的图象所在的象限,进而可得出结论.
解答 解:∵反比例函数y=-$\frac{5}{x}$中,k=-5<0,
∴此函数图象的两个分支分别位于二四象限.
∵-1<0,2>0,
∴点A(-1,y1)位于第二象限,点B(2,y2)位于第四象限,
∴y1>0,y2<0,
∴y2<0<y1.
故选B.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
10.同学们学习多项式后,老师在黑板上写了一道题目:任意写一个含有字母a,b的四次三项式,其中最高次项的系数为-2,常数项为8,则所写出符合要求的多项式是( )
| A. | 3a-2ab3+8 | B. | 2a2b2+8 | C. | -2a3b-8a-8 | D. | -2a4-b-8 |
 如图,正方形ABCD的边长为2,E是BC的中点,将△ABE绕点A顺时针旋转90°,设点E的对应点为F.
如图,正方形ABCD的边长为2,E是BC的中点,将△ABE绕点A顺时针旋转90°,设点E的对应点为F.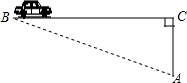 超速行驶是引发交通事故的主要原因之一,上周末,小明和三位同学尝试用自己所学的知识检测车速,如图8,观测点设在A处,离娄新高速的距离(AC)为30m,这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为4s,∠BAC=75°.
超速行驶是引发交通事故的主要原因之一,上周末,小明和三位同学尝试用自己所学的知识检测车速,如图8,观测点设在A处,离娄新高速的距离(AC)为30m,这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为4s,∠BAC=75°.