题目内容
 直线y=
直线y=| 4 |
| 3 |
(1)点N的坐标;
(2)直线AM的函数表达式.
考点:翻折变换(折叠问题),待定系数法求一次函数解析式
专题:
分析:(1)由△ABM沿AM折叠,点B恰好落在x轴上的N处得到AB=AN,而AB的长度根据已知可以求出,所以N点的坐标由此求出;
(2)由于折叠得到NM=BM,在直角△NMO中根据勾股定理可以求出OM,也就求出M的坐标,而A的坐标已知,由此即可求出直线AM的解析式.
(2)由于折叠得到NM=BM,在直角△NMO中根据勾股定理可以求出OM,也就求出M的坐标,而A的坐标已知,由此即可求出直线AM的解析式.
解答:解:(1)∵直线y=
x+8与x轴、y轴分别交于A和B,
∴A(-6,0)、B(0,8),
∴OA=6,OB=8,
∴AB=10,
而△ABM沿AM折叠,点B恰好落在x轴上的C处
∴AB=AN=10,
∴N(4,0);
(2)设M(0,b),
则NM=BM=8-b,
∵NM2=NO2+OM2,
∴b=3,
∴M(0,3),而A(-6,0),
设直线AM的解析式为y=kx+b(k≠0),
,
解得,
∴直线AM的解析式为:y=
x+3.
| 4 |
| 3 |
∴A(-6,0)、B(0,8),
∴OA=6,OB=8,
∴AB=10,
而△ABM沿AM折叠,点B恰好落在x轴上的C处
∴AB=AN=10,
∴N(4,0);
(2)设M(0,b),
则NM=BM=8-b,
∵NM2=NO2+OM2,
∴b=3,
∴M(0,3),而A(-6,0),
设直线AM的解析式为y=kx+b(k≠0),
|
解得,
|
∴直线AM的解析式为:y=
| 1 |
| 2 |
点评:本题综合考查了一次函数图象和性质与几何知识的应用,题中利用折叠知识与直线的关系以及直角三角形等知识求出线段的长是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 如图,在菱形ABCD中,∠ABC=60°,过点A作AE⊥CD于点E,交对角线BD于点F,过点F作FG⊥AD于点G.
如图,在菱形ABCD中,∠ABC=60°,过点A作AE⊥CD于点E,交对角线BD于点F,过点F作FG⊥AD于点G.  如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.
如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.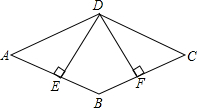 如图,四边形ABCD是菱形,DE⊥AB于E,EF⊥BC于F.求证:DE=DF.
如图,四边形ABCD是菱形,DE⊥AB于E,EF⊥BC于F.求证:DE=DF. 如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运输费15000元,铁路运输费97200元.请计算这批产品的销售款比原料费和运输费的和多多少元?
如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运输费15000元,铁路运输费97200元.请计算这批产品的销售款比原料费和运输费的和多多少元? 已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.求证:BE∥CF.
已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.求证:BE∥CF. 如图,菱形ABCD中,∠BAD=120°,CF⊥AD于点E,且BC=CF,连接BF交对角线AC于点M,则∠FMC=
如图,菱形ABCD中,∠BAD=120°,CF⊥AD于点E,且BC=CF,连接BF交对角线AC于点M,则∠FMC=