题目内容
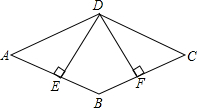如图，四边形ABCD是菱形，DE⊥AB于E，EF⊥BC于F．求证：DE=DF．考点：菱形的性质
专题：证明题
分析：利用菱形的性质得出∠EBD=∠FBD，进而求出△DEB≌△DFB（AAS），进而得出答案．
解答：
证明：连接BD，
∵四边形ABCD是菱形，
∴∠EBD=∠FBD，
在△DEB和△DFB中
，
∴△DEB≌△DFB（AAS），
∴DE=DF．
证明：连接BD，∵四边形ABCD是菱形，
∴∠EBD=∠FBD，
在△DEB和△DFB中
|
∴△DEB≌△DFB（AAS），
∴DE=DF．
点评：此题主要考查了全等三角形的判定与性质以及菱形的性质等知识，得出△DEB≌△DFB（AAS）是解题关键．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
如图是交警在某个路口统计的某时段来往车辆的车速情况．（单位：千米/时）
直线y=