题目内容
6. 如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3.
如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3.
分析 设P(x,y),则y=$\frac{9}{2x}$,利用勾股定理得到OP2=x2+y2=x2+$\frac{81}{4{x}^{2}}$,再根据不等式公式得x2+$\frac{81}{4{x}^{2}}$≥2$\sqrt{{x}^{2}•\frac{81}{4{x}^{2}}}$,所以OP2≥9,于是可判断OP的最小值为3.
解答 解:设P(x,y),则y=$\frac{9}{2x}$,
所以OP2=x2+y2=x2+$\frac{81}{4{x}^{2}}$,
∵x2+$\frac{81}{4{x}^{2}}$≥2$\sqrt{{x}^{2}•\frac{81}{4{x}^{2}}}$,
∴OP2≥9,
∴OP≥3,
∴OP的最小值为3.
即P到原点的最小距离为3.
故答案为3.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了a+b≥2$\sqrt{ab}$(a>0,b>0,当a=b时取等号).

练习册系列答案
相关题目
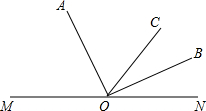 如图,点M,O,N在同一直线上,射线OA和射线OB分别平分∠MOC和∠NOC,∠AOB是什么角?请说明理由.
如图,点M,O,N在同一直线上,射线OA和射线OB分别平分∠MOC和∠NOC,∠AOB是什么角?请说明理由. 如图,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.求:
如图,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.求: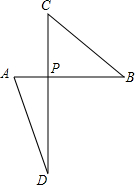 如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.
如图,点P是线段AB的黄金分割点,将线段PB绕着点P逆时针旋转90°到点C,延长CP到点D.使PD=AB.连接AD,试比较△PCB与△PAD的面积大小,并说明理由.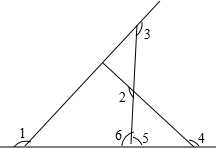 如图,求∠1+∠2+∠3+∠4的度数.
如图,求∠1+∠2+∠3+∠4的度数.