题目内容
16.根据如图中所注的条件,判断图中两个三角形是否相似,并求出x和y的值.
分析 (1)由∠G=∠I=90°,直接利用勾股定理即可求得x与y的值,然后利用三组对应边的比相等的两个三角形相似证得结论.
(2)先证出$\frac{FH}{JH}=\frac{GH}{KH}$,再求出∠FHG=∠JHK,即可得出△FGH∽△JKH,由相似三角形的性质即可求出x和y的值.
解答 解:(1)相似.
∵∠G=∠I=90°,
∴x=GH=$\sqrt{F{H}^{2}-F{G}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,y=HJ=$\sqrt{H{I}^{2}+I{J}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴$\frac{FG}{IJ}=\frac{GH}{HI}$=$\frac{1}{2}$,
∴△FGH∽△JIH.
(2)相似.
∵$\frac{FH}{JH}=\frac{72}{48}$=$\frac{3}{2}$,$\frac{GH}{KH}=\frac{48}{32}$=$\frac{3}{2}$,
∴$\frac{FH}{JH}=\frac{GH}{KH}$,
∵∠FHK=∠GHJ=90°,
∴∠FHG=∠JHK,
∴△FGH∽△JKH,
∴∠G=∠K,$\frac{GF}{KJ}$=$\frac{3}{2}$,
即x°=124°,$\frac{y}{22}=\frac{3}{2}$,
∴x=124,y=33.
点评 此题考查了相似三角形的判定与性质、勾股定理;熟练掌握相似三角形的判定定理是解决问题的关键.

练习册系列答案
相关题目
11.丽英是山区的孩子,她的家和学校在两座相邻的山顶上,去学校时先下坡再上坡,下坡路占全程的$\frac{1}{3}$,下坡速度是上坡速度的2倍,从家走到学校要花2个半小时,那么她从学校回家需要多少时间?( )
| A. | 2小时40分 | B. | 2个半小时 | C. | 2小时 | D. | 1小时40分 |
1.在某复印社复印文件,复印页数不超过50时,每页收费0.11元,超过部分每页收费降为0.08元.在某图书馆复印同样的文件,不论复印多少页,每页收费0.09元.
设需要复印文件x页(x为正整数),请根据表中提供的信息回答下列问题:
(1)用含有x的式子填写如表:
(2)当x为何值时,两种收费相等;
(3)当你有一本书要复印、页码共有200页,你认为在哪里复印省钱?(直接写出结果即可)
设需要复印文件x页(x为正整数),请根据表中提供的信息回答下列问题:
(1)用含有x的式子填写如表:
| x≤50 | x>50 | |
| 复印店计费/元 | 0.11x | 0.08x+1.5 |
| 图书馆计费/元 | 0.09x | 0.09x |
(3)当你有一本书要复印、页码共有200页,你认为在哪里复印省钱?(直接写出结果即可)
 如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3.
如图,P是反比例函数y=$\frac{9}{2x}$(k>0)第一象限的图象上的一点,则P到原点的最小距离为3.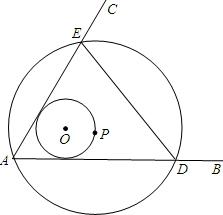 如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$.
如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$.