题目内容
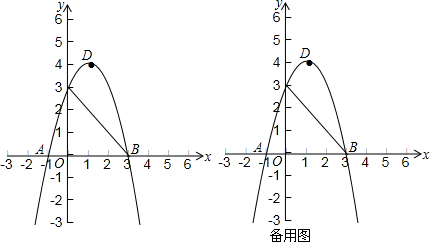
11.如图,已知抛物线y=-x2+bx+c,与x轴交于点A、B,且点A的坐标为(-1,0),与y轴交于点C(0,3),D为抛物线的顶点.(1)求抛物线的解析式及D点的坐标;
(2)P为第一象限内抛物线上一点,过点P作x轴的垂线,垂足为N,PN交线段BC于M,连接PC、PB,设P点的横坐标为t,△PBC的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,连接OM,当t为何值时,△OMN与△CDB相似.
分析 (1)代入点A(-1,0),点C(0,3)求得函数解析式即可;进一步利用顶点坐标公式求得答案即可;
(2)设P点的横坐标为t,纵坐标为-t2+2t+3,利用三角形PBN的面积加上梯形CONP的面积减去三角形OBC的面积表示出三角形PBC的面积即可;
(3)利用勾股定理分别求得DC、DB、BC的长,利用勾股定理逆定理判定三角形BCD是直角三角形,求得BC解析式,设出M点的坐标,再利用三角形相似的性质分两种直角边对应求得答案即可.
解答 解:(1)把A(-1,0),C(0,3)代入y=-x2+bx+c,
解得b=2,c=3,
抛物线的解析式为y=-x2+2x+3;
-$\frac{2}{2×(-1)}$=1,$\frac{4×(-1)×3-{2}^{2}}{-4}$=4,
顶点D为(1,4);
(2)如图,
由题意可知点P(t,-t2+2t+3)
S=$\frac{1}{2}$(3-t)(-t2+2t+3)+$\frac{1}{2}$t(3-t2+2t+3)-$\frac{1}{2}$×3×3
=-$\frac{3}{2}$t2+$\frac{9}{2}$t;
(3)如图,
由题意可知:BC=3$\sqrt{2}$,CD=$\sqrt{2}$,BD=2$\sqrt{5}$,
∵BC2+CD2=BD2,
∴△BCD是直角三角形,∠BCD=90°,
∵B(3,0),C(0,3),
∴直线BC=-x+3,
设M点的坐标为(t,-t+3),
∵△OMN∽△CDB,
∴$\frac{ON}{CD}$=$\frac{MN}{BC}$或$\frac{MN}{CD}$=$\frac{ON}{BC}$,
即$\frac{t}{\sqrt{2}}$=$\frac{-t+3}{3\sqrt{2}}$或$\frac{-t+3}{\sqrt{2}}$=$\frac{t}{3\sqrt{2}}$
解得$t=\frac{3}{4}$或$t=\frac{9}{4}$.
点评 此题考查二次函数综合题,综合考查了待定系数法求函数解析式,勾股定理,勾股定理逆定理的运用,相似的性质,以及渗透分类讨论思想.

 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 1.4 |
| A. | 1 | B. | -1 | C. | 4 | D. | -7 |
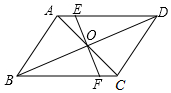 如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.