题目内容
1.已知一元二次方程ax2+bx+c=0(a≠0)中,如果b2-4ac≥0,那么它的两个实数根是x1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,x2=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$.(1)计算:x1+x2、x1x2的值(用含a、b、c的代数式表示);
(2)设方程2x2-4x-1=0的两个根分别为x1、x2,根据(1)所求的结果,不解方程直接写出x1+x2=2,x1x2=-$\frac{1}{2}$.
(3)如果方程2x2-4x+c=0的一根是2+$\sqrt{3}$,请你利用(1)中根与系数的关系求出方程的另一根及c的值.
分析 (1)把x1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,x2=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$代入x1+x2、x1x2即可得到结果;
(2)根据(1)中的结果代入即可得到结论;
(3)根据(1)中的结果,把系数代入即可得到结论.
解答 解:(1)x1+x2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=-$\frac{b}{a}$,
x1x2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$•$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{(-b)^{2}-(\sqrt{{b}^{2}-4ac)^{2}}}{4{a}^{2}}$=$\frac{c}{a}$;
(2)∵方程2x2-4x-1=0的两个根分别为x1、x2,
∴x1+x2=-$\frac{-4}{2}$=2,x1•x2=$\frac{-1}{2}$=-$\frac{1}{2}$;
故答案为:2,-$\frac{1}{2}$;
(3)方程的另一根为x1,
∴x1+2+$\sqrt{3}$=2,x1(2+$\sqrt{3}$)=$\frac{c}{2}$,
解得:x1=$\sqrt{3}$,c=4$\sqrt{3}$+6.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
12.2014年石家庄6月21至30日的空气质量指数分别为:112,115,101,147,181,189,112,83,95,103,则这10天空气质量指数的平均数是( )
| A. | 133.8 | B. | 123.8 | C. | 133.6 | D. | 123.6 |
13.下列无理数中,在-1与2之间的是( )
| A. | -$\sqrt{3}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
11.如图,图(1)的正方形的周长与图(2)的长方形的周长相等,且长方形的长比宽多x,则正方形的面积与长方形的面积的差为( )
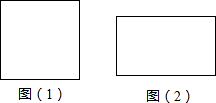

| A. | x2 | B. | $\frac{1}{2}{x}^{2}$ | C. | $\frac{1}{3}{x}^{2}$ | D. | $\frac{1}{4}$x2 |
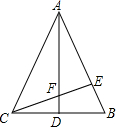 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,在AB上取一点E,连接CE,交AD于点F.若BE=2,BC=6,∠CAD=∠BCE.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,在AB上取一点E,连接CE,交AD于点F.若BE=2,BC=6,∠CAD=∠BCE.