题目内容
14.代数式$\sqrt{a+4}$-$\sqrt{9-2a}$+$\sqrt{1-3a}$+$\sqrt{-{a}^{2}}$是否存在确定的值?若存在,求出代数式的值;若不存在,请说明理由.分析 根据二次根式的意义,被开方数是非负数,列不等式组解得结果,得出结论.
解答 解:由题意得:
$\left\{\begin{array}{l}{a+4≥0}\\{9-2a≥0}\\{1-3a≥0}\\{{-a}^{2}≥0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a≥-4}\\{a≤\frac{9}{2}}\\{a≤\frac{1}{3}}\\{a=0}\end{array}\right.$,
∴此不等式组无解,
∴原代数式不存在确定的值.
点评 本题主要考查了二次根式有意义的条件,掌握被开方数是非负数是解答此题的关键.

练习册系列答案
相关题目
2.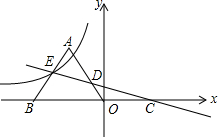 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )| A. | -$\frac{6}{7}$ | B. | -$\sqrt{3}$ | C. | -3 | D. | -4 |
4.下列各图中,∠1与∠2是内错角的是( )
| A. | 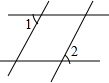 | B. | 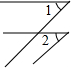 | C. | 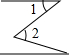 | D. | 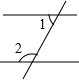 |
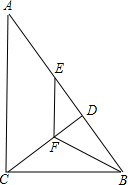 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
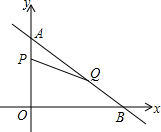 如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒. 计算下图阴影部分面积:
计算下图阴影部分面积: