题目内容
11.已知:a,b互为相反数,c,d互为倒数,x=3(a-1)-(a-2b),y=c2d+d2-($\frac{d}{c}$+c-2),求:$\frac{2x-y}{3}$-$\frac{3x+2y}{6}$的值.分析 根据题意得a+b=0,cd=1,求得x,y,再代入$\frac{2x-y}{3}$-$\frac{3x+2y}{6}$,求值即可.
解答 解:∵a,b互为相反数,c,d互为倒数,
∴a+b=0,cd=1,
∴x=3(a-1)-(a-2b)=3a-3-a+2b=2a+2b-3=2(a+b)-3=-3,
y=c2d+d2-($\frac{d}{c}$+c-2)=c2d+d2-d2-c+2=2,
原式=$\frac{2(2x-y)}{6}$-$\frac{3x+2y}{6}$
=$\frac{4x-2y-3x-2y}{6}$
=$\frac{x-4y}{6}$;
当x=-3,y=2时,原式=$\frac{-3-4×2}{6}$=-$\frac{11}{6}$.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.一元二次方程x2=5x的根是( )
| A. | x=5 | B. | x=0 | C. | x1=0,x2=5 | D. | 以上答案都不对 |
1.下列计算正确的是( )
| A. | a+a=a2 | B. | 6a3-5a2=a | C. | 3a2+2a3=5a5 | D. | 3a2b-4ba2=-a2b |
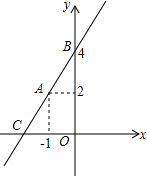 如图,一次函数的图象经过平面直角坐标系中A、B两点.
如图,一次函数的图象经过平面直角坐标系中A、B两点.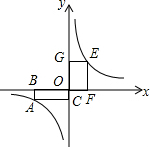 如图A、E是双曲线y=$\frac{4}{x}$上的两点,过A点作AB⊥x轴于B,AC⊥x轴于B轴于F,EG⊥y轴于G,则SABOC+SEFOG的值为( )
如图A、E是双曲线y=$\frac{4}{x}$上的两点,过A点作AB⊥x轴于B,AC⊥x轴于B轴于F,EG⊥y轴于G,则SABOC+SEFOG的值为( )