题目内容
1．
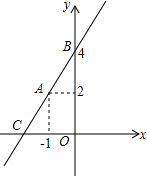如图，一次函数的图象经过平面直角坐标系中A、B两点．（1）求一次函数解析式；
（2）当x=5时，求y的值；
（3）求一次函数图象与坐标轴围成的△BOC的面积．
分析 （1）把（-1，2）和（0，4）代入解析式解答即可；
（2）把x=5代入解析式解答即可；
（3）把y=0代入解析式得出点C的坐标，利用三角形面积公式解答即可．
解答 解：（1）把（-1，2）和（0，4）代入解析式y=kx+b，
可得：$\left\{\begin{array}{l}{-k+b=2}\\{b=4}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$，
所以解析式为：y=2x+4，
（2）把x=5代入y=2x+4=14，
（3）把y=0代入y=2x+4，解得：x=-2，
所以△BOC的面积=$\frac{1}{2}×2×4=4$
点评 此题主要考查了一次函数问题，关键是根据一次函数图象上点的坐标特点进行解答．
练习册系列答案
相关题目
11．若$\frac{x}{y}$=$\frac{4}{5}$，则$\frac{2x-y}{x+y}$的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 1 | D． | $\frac{3}{2}$ |
13．下列二次根式是最简二次根式的是（ ）
| A． | $\sqrt{{a}^{2}x+{a}^{3}y}$ | B． | $\sqrt{\frac{1}{3}}$ | C． | $\sqrt{18}$ | D． | $\sqrt{{a}^{2}-{b}^{2}}$ |