题目内容
15.计算:(1)2$\sqrt{12}$-6$\sqrt{27}$+4$\sqrt{48}$
(2)($\sqrt{0.5}$-2$\sqrt{\frac{1}{3}}$)-($\sqrt{\frac{1}{8}}$-$\sqrt{75}$)
分析 (1)根据二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并;
(2)根据去括号的法则,可去括号,根据二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.
解答 解:(1)原式=4$\sqrt{3}$-18$\sqrt{3}$+16$\sqrt{3}$=2$\sqrt{3}$;
(2)原式=$\sqrt{0.5}$-2$\sqrt{\frac{1}{3}}$-$\sqrt{\frac{1}{8}}$+$\sqrt{75}$=$\frac{\sqrt{2}}{2}$-$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{2}}{4}$+5$\sqrt{3}$=$\frac{\sqrt{2}}{4}$+$\frac{13\sqrt{3}}{3}$.
点评 本题考查了二次根式的加减,同类二次根式是指几个二次根式化简成最简二次根式后,被开方数相同的二次根式.二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
5.用长为16m的木条围成一个矩形框架,设矩形面积为S(m2),则S的最大值为( )
| A. | 8m2 | B. | 16m2 | C. | 12m2 | D. | 32m2 |
7.把分式$\frac{2a}{a+b}$中的a、b都扩大5倍,则分式的值( )
| A. | 扩大10倍 | B. | 不变 | C. | 扩大5倍 | D. | 缩小5倍 |
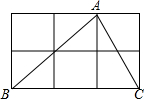 如图,△ABC的3个顶点分别在小正方形的顶点上,这样的三角形叫做格点三角形,在图中再画格点三角形(位置不同于△ABC),使得所画三角形与△ABC全等,则这样的格点三角形能画( )
如图,△ABC的3个顶点分别在小正方形的顶点上,这样的三角形叫做格点三角形,在图中再画格点三角形(位置不同于△ABC),使得所画三角形与△ABC全等,则这样的格点三角形能画( )