题目内容
16.已知△ABC与△DEF相似,且∠A=∠E,如果AB=16,AC=12,DF=6,EF=4,那么BC=24或18.分析 根据△ABC与△DEF相似,且∠A=∠E,分两种情况讨论:△ABC∽△EFD,△ABC∽△EDF,分别根据对应边成比例,求得BC的长.
解答 解:∵△ABC与△DEF相似,且∠A=∠E,
∴当△ABC∽△EFD时,$\frac{BC}{DF}$=$\frac{AB}{EF}$,
即$\frac{BC}{6}$=$\frac{16}{4}$,
解得BC=24;
当△ABC∽△EDF时,$\frac{BC}{FD}$=$\frac{AC}{EF}$,
即$\frac{BC}{6}$=$\frac{12}{4}$,
解得BC=18.
故答案为:24或18.
点评 本题主要考查了相似三角形的性质的运用,解题时注意:相似三角形的对应角相等,对应边的比相等.

练习册系列答案
相关题目
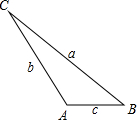 如图,已知△ABC中,∠B=2∠C,a,b,c为三边长.
如图,已知△ABC中,∠B=2∠C,a,b,c为三边长.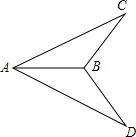 如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.
如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.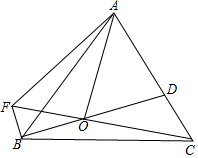 如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.
如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.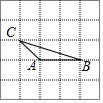 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )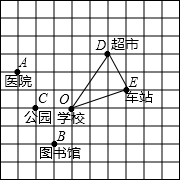 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题: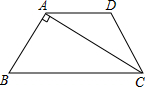 如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,tan∠DCA=$\frac{3}{4}$,AC=8,则AB的值是6.
如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,tan∠DCA=$\frac{3}{4}$,AC=8,则AB的值是6.