题目内容
4.如图1,CA=CB,CD=CE,∠ACB=∠DCE=90°,D,C,B在一条直线上,F,G分别是BE,AD的中点,(1)求证:BE=AD;
(2)求∠CFG的度数;
(3)将图1中的△CED绕点C旋转至图2的位置,请完成作图,并求出∠CFG的度数.

分析 (1)由SAS证得△ACD≌△BCE,即可得出结论;
(2)连接CG,由(1)与F,G分别是BE,AD的中点,得出AG=BF,∠CAG=∠CBF,由SAS证得△AGC≌△BFC,得出CG=CF,∠BCF=∠ACG,求得∠GCF=90°,得出△GCF为等腰直角三角形即可得出结果;
(3)连接CG,由SAS证得△ACD≌△BCE,得出BE=AD,AG=BF,∠CAG=∠CBF,由SAS证得AGC≌△BFC(SAS得出CG=CF,∠BCF=∠ACG,求得∠GCF=90°,得出△GCF为等腰直角三角形即可得出结果.
解答 (1)证明:在△ACD和△BCE中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACB=∠DCE=90°}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),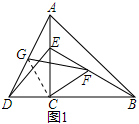
∴BE=AD;
(2)解:连接CG,如图1所示:
∵F,G分别是BE,AD的中点,
∴AG=$\frac{1}{2}$AD,BF=$\frac{1}{2}$BE,
∵BE=AD,
∴AG=BF,
∵△ACD≌△BCE,
∴∠CAG=∠CBF,
在△AGC和△BFC中,
$\left\{\begin{array}{l}{CA=CB}\\{∠CAG=∠CBF}\\{AG=BF}\end{array}\right.$,
∴△AGC≌△BFC(SAS),
∴CG=CF,∠BCF=∠ACG,
∵∠BCF+∠ECF=∠ACB=90°,
∴∠ACG+∠ECF=90°,
即∠GCF=90°,
∴△GCF为等腰直角三角形,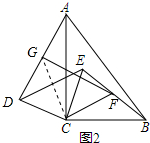
∴∠CFG=45°;
(3)解:连接CG,如图2所示:
在△ACD和△BCE中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE=90°-∠ACE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴BE=AD,
∵F,G分别是BE,AD的中点,
∴AG=BF,
∵△ACD≌△BCE,
∴∠CAG=∠CBF,
在△AGC和△BFC中,
$\left\{\begin{array}{l}{CA=CB}\\{∠CAG=∠CBF}\\{AG=BF}\end{array}\right.$,
∴△AGC≌△BFC(SAS),
∴CG=CF,∠BCF=∠ACG,
∵∠BCF+∠ACF=∠ACB=90°,
∴∠ACG+∠ACF=90°,
即∠GCF=90°,
∴△GCF为等腰直角三角形,
∴∠CFG=45°.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、旋转的性质、线段的中点的性质等知识;难度较大,特别是(2)、(3)中,需作辅助线并多次证明三角形全等才能得出结果.

 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
| x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;

②当t为何值时,乒乓球达到最大高度?
(2)如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少?
| A. | 球 | B. | 圆柱 | C. | 棱柱 | D. | 圆锥 |
 如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )
如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )| A. | 45° | B. | 60° | C. | 90° | D. | 100° |
 如图所示,△ABD,△ACE都是等边三角形,点C在BD上,则∠ADE=60°.
如图所示,△ABD,△ACE都是等边三角形,点C在BD上,则∠ADE=60°. 如图所示,线段AD、BC、EF相交于点O,EO=FO,AB∥CD,试证明:AB=CD.
如图所示,线段AD、BC、EF相交于点O,EO=FO,AB∥CD,试证明:AB=CD. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB上的一个动点,DE⊥AC于点E.DF⊥BC于点F,点D从点A出发向点B移动(不含A、B两点),若AD长为x,矩形DECF的周长为y,则下列图象能大致反映y与x的函数关系的是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB上的一个动点,DE⊥AC于点E.DF⊥BC于点F,点D从点A出发向点B移动(不含A、B两点),若AD长为x,矩形DECF的周长为y,则下列图象能大致反映y与x的函数关系的是( )


