题目内容
6. 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
| x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;

②当t为何值时,乒乓球达到最大高度?
(2)如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少?
分析 (1)①根据描出了上表中y与t各对对应值为坐标的点,画出该函数的图象即可;
②利用网格中数据直接得出乒乓球达到最大高度时的时间;
(2)首先求出函数解析式,进而求出乒乓球落在桌面时,与端点A的水平距离.
解答 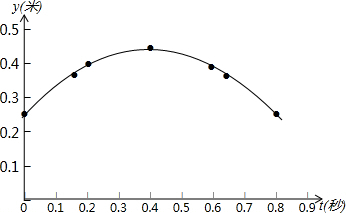 解:(1)①如图所示,
解:(1)①如图所示,
②由表格中数据可得,t=0.4(秒),乒乓球达到最大高度;
(2)由表格中数据,可设y=a(x-1)2+0.45,
将(0,0.25)代入,可得:a=-$\frac{1}{5}$,
则y=-$\frac{1}{5}$(x-1)2+0.45,
当y=0时,0=-$\frac{1}{5}$(x-1)2+0.45,
解得:x1=$\frac{5}{2}$,x2=-$\frac{1}{2}$(舍去),
即乒乓球与端点A的水平距离是$\frac{5}{2}$m.
点评 此题主要考查了二次函数对应用以及根的判别式和一元二次方程的解法等知识,利用图表中数据得出函数解析式是解题关键.

练习册系列答案
相关题目
17.下列语句中不是命题的有( )
(1)两点之间,直线最短;
(2)不许大声讲话;
(3)连结A,B两点;
(4)鸟是动物;
(5)相等的角是对顶角;
(6)无论n为怎样的自然数,式子n2-n+11的值都是质数吗?
(1)两点之间,直线最短;
(2)不许大声讲话;
(3)连结A,B两点;
(4)鸟是动物;
(5)相等的角是对顶角;
(6)无论n为怎样的自然数,式子n2-n+11的值都是质数吗?
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.对于反比例函数$y=\frac{2}{x}$,下列说法正确的是( )
| A. | 图象经过点(2,-1) | B. | 图象位于第二、四象限 | ||
| C. | 当x<0时,y随x的增大而减小 | D. | 当x>0时,y随x的增大而增大 |
 在平面直角坐标系xOy中,抛物线$y=\frac{1}{2}{x^2}+bx+c$经过点A(0,2)和B(1,$\frac{3}{2}$).
在平面直角坐标系xOy中,抛物线$y=\frac{1}{2}{x^2}+bx+c$经过点A(0,2)和B(1,$\frac{3}{2}$). 如图,点C在线段AB上,AC:BC=3:2,点M是AB的中点,点N是BC的中点,若MN=3cm,求线段AB的长.
如图,点C在线段AB上,AC:BC=3:2,点M是AB的中点,点N是BC的中点,若MN=3cm,求线段AB的长.