题目内容
16. 如图,AB=AD,AC=AE,∠BAD=∠CAE=90°,点F为DE的中点,求证:BC=2AF.
如图,AB=AD,AC=AE,∠BAD=∠CAE=90°,点F为DE的中点,求证:BC=2AF.
分析 延长AF到M,使AF=MF,连接DM,EM(如图),根据对角线互相平分的四边形是平行四边形,得到ADME为平行四边形,然后根据平行四边形的性质得到DM=AE=AC,∠ADM+∠DAE=180°,再由已知的∠BAD=∠CAE=90°得到∠BAC+∠DAE=180°,从而得到∠ADM=∠BAC,再由AB=AD,利用SAS求证△MDA≌△CAB,最后根据全等三角形的对应边相等即可得证.
解答 证明:延长AF到M,使AF=MF,连接DM,EM(如图)
∵AF=MF,DF=EF,
∴四边形ADME为平行四边形.
∴DM=AE=AC,∠ADM+∠DAE=180°
又∵∠BAD=∠CAE=90°,
∴∠BAC+∠DAE=180°,
∴∠ADM=∠BAC,
在△MDA和△CAB中,
$\left\{\begin{array}{l}{DM=AC}\\{∠ADM=∠BAC}\\{AD=AB}\end{array}\right.$
∴△MDA≌△CAB(SAS),
∴BC=AM,
∵AM=2AF,
∴BC=2AF.
点评 此题考查学生对等腰三角形的判定与性质,三角形内角和定理,全等三角形的判定与性质的理解和掌握,解答此题的关键是延长AF到M,使AF=MF,连接DM,EM,求证两次三角形全等,即可证明BC=2AF.

练习册系列答案
相关题目
6.已知$\left\{\begin{array}{l}{a+2b=3c}\\{2a-3b=-8c}\end{array}\right.$,求$\frac{3a+4b+c}{4a-3b+2c}$的值.
6.在Rt△ABC中,∠C=90°,AB=10,BC=8,则cosA=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$. |

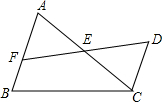 如图,AB∥CD,EF=ED,AB=5,CD=3,则BF=2.
如图,AB∥CD,EF=ED,AB=5,CD=3,则BF=2. 如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.
如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.