题目内容
20.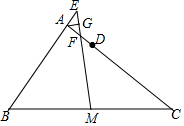 如图,在△ABC中,D为AC上一点,AB=CD,F是AD的中点,M为BC的中点,连结MF并延长交BA延长线于点E,G为EF的中点,求证:AG⊥ME.
如图,在△ABC中,D为AC上一点,AB=CD,F是AD的中点,M为BC的中点,连结MF并延长交BA延长线于点E,G为EF的中点,求证:AG⊥ME.
分析 连接BD,取BD的中点为O,连接FO,MO,易证MO是△BCD的中位线,FO是△ABD的中位线,进而可证明MO∥AC,OF∥AB,再证明∠AEF=∠AFE,由此可得AE=AF,最后根据等腰三角形的性质即可证明AG⊥ME.
解答 证明:
连接BD,取BD的中点为O,连接FO,MO ,
,
∵F是AD的中点,M为BC的中点,
∴MO是△BCD的中位线,FO是△ABD的中位线,
∴MO=$\frac{1}{2}$CD,FO=$\frac{1}{2}$AB,MO∥AC,OF∥AB,
∵AB=CD,
∴MO=FO,
∴∠OFM=∠OMF,
∵OF∥AB,
∴∠OFM=∠AEF,
∵OM∥AC,
∴∠OMF=∠CFM=∠AFE,
∴∠AEF=∠AFE,
∴AE=AF,
∵G为EF的中点,
∴AG⊥ME.
点评 本题考查了三角形的中位线定理、等腰三角形的判断和性质,解答本题的关键是正确作出辅助线,有一定难度.

练习册系列答案
相关题目
9.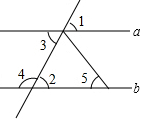 如图,在下列条件中,不能判定直线a与b平行的是( )
如图,在下列条件中,不能判定直线a与b平行的是( )
 如图,在下列条件中,不能判定直线a与b平行的是( )
如图,在下列条件中,不能判定直线a与b平行的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠3+∠4=180° | D. | ∠3=∠5 |
10.下列说法不一定成立的是( )
| A. | 若a>b,则a+c>b+c | B. | 若a+c>b+c,则a>b | C. | 若a>b,则a2c>bc2 | D. | 若a2c>bc2,则a>b |

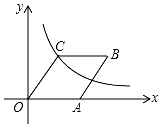 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
 已知小明家5月份总支出共计5000元,各项支出所占百分比如图所示,那么用于教育的支出是900元.
已知小明家5月份总支出共计5000元,各项支出所占百分比如图所示,那么用于教育的支出是900元.