题目内容
17.等腰三角形一腰上的高与另一腰的夹角为50°,则这条高与底边夹角的度数为20°或70°.分析 从锐角三角形和钝角三角形两种情况,利用三角形内角和定理先求出它的底角的度数,再求出腰上的高与底边的夹角的度数.
解答 解:在三角形ABC中,设AB=AC,BD⊥AC于D,∠ABD=40°.
①若是锐角三角形,∠A=90°-50°=40°,
∠ABC=∠C=(180°-40°)÷2=70°,
∠DBC=∠ABC-∠ABD=20°;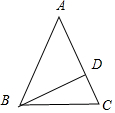
②若三角形是钝角三角形,∠BAC=50°+90°=140°,
此时∠ABC=∠C=(180°-140°)÷2=20°,
∠DBC=∠ABC+∠ABD=70°.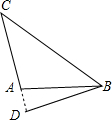
所以腰上的高与底边的夹角的度数是70°或20°.
故答案为20°或70°.
点评 此题主要考查学生对等腰三角形的性质和三角形内角和定理的理解和应用,此题的关键是熟练掌握三角形内角和定理.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
7.某区的绿化覆盖率由如下统计数据:
如果以后的几年继续依此速度发展绿化.
(1)观察此表格,第5年年底的绿化覆盖率为多少?
(2)探索规律,问第10年年底的绿化覆盖率为多少?第n年年底的绿化覆盖率为多少?﹙n≤35的正整数﹚
| 年份 | 第1年年底 | 第2年年底 | 第3年年底 | 第4年年底 |
| 绿化覆盖率﹙%﹚ | 22.2 | 23.8 | 25.4 | 27.0 |
| 年份 | 第5年年底 | … | 第10年年底 | |
| 绿化覆盖率﹙%﹚ |
(1)观察此表格,第5年年底的绿化覆盖率为多少?
(2)探索规律,问第10年年底的绿化覆盖率为多少?第n年年底的绿化覆盖率为多少?﹙n≤35的正整数﹚
2.某水果批发商店为了考察1000筐苹果的等次,从中抽取了50筐进行检查,下面说法正确的是( )
| A. | 总体是1000筐苹果 | B. | 样本是50筐苹果 | ||
| C. | 总体是指1000筐苹果的等次 | D. | 样本是指苹果的等次 |

 已知小明家5月份总支出共计5000元,各项支出所占百分比如图所示,那么用于教育的支出是900元.
已知小明家5月份总支出共计5000元,各项支出所占百分比如图所示,那么用于教育的支出是900元.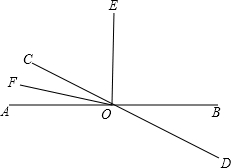 如图,已知直线AB,CD相交于点O,OE,OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求:
如图,已知直线AB,CD相交于点O,OE,OF为射线,∠AOE=90°,OF平分∠AOC,∠AOF+∠BOD=51°,求: