题目内容
某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6080元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
(1)现该商场要保证每天盈利6080元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
考点:二次函数的应用
专题:
分析:(1)设每千克水果涨了x元,那么就少卖了20x千克,根据市场每天销售这种水果盈利了6 080元,同时顾客又得到了实惠,可列方程求解;
(2)利用总利润y=销量×每千克利润,进而求出最值即可.
(2)利用总利润y=销量×每千克利润,进而求出最值即可.
解答:解:(1)设每千克水果涨了x元,
(10+x)(500-20x)=6080,
解得:x1=6,x2=9.
因为要顾客得到实惠,所以应该上涨6元.
(2)设总利润为y,则:y=(10+x)(500-20x)=-20x2+300x+5000=-20(x-
)2+6125,
即每千克这种水果涨价7.5元,能使商场获利最多.
(10+x)(500-20x)=6080,
解得:x1=6,x2=9.
因为要顾客得到实惠,所以应该上涨6元.
(2)设总利润为y,则:y=(10+x)(500-20x)=-20x2+300x+5000=-20(x-
| 15 |
| 2 |
即每千克这种水果涨价7.5元,能使商场获利最多.
点评:此题主要考查了二次函数的应用以及一元二次方程的解法,正确得出y与x的函数关系式是解题关键.

练习册系列答案
相关题目
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
⊙O的半径为2,则它的内接正六边形的边长为( )
| A、2 | ||
B、2
| ||
C、
| ||
D、2
|
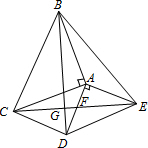 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG=
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG= 把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP=
把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP= 如图,点C是AB的中点,点D是BC的中点,AB=28,求线段AD的长.
如图,点C是AB的中点,点D是BC的中点,AB=28,求线段AD的长. 一只蚂蚁从长为4cm,高时5cm的长方体纸箱的A点沿纸箱跑到B点,有不同的爬行路线.画出平面图示(相同类型画一个),并通过计算说明哪条线路最短,最短路线长多少?
一只蚂蚁从长为4cm,高时5cm的长方体纸箱的A点沿纸箱跑到B点,有不同的爬行路线.画出平面图示(相同类型画一个),并通过计算说明哪条线路最短,最短路线长多少?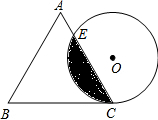 如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E.
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E.