题目内容
10．一项工程，甲单独做需a天完成，乙单独做需b天完成，现两人合做，完成这项工程所需的天数为$\frac{ab}{a+b}$．分析 要把工作总量看作单位1，甲、乙两人合做完成这项工程的天数=1÷（甲乙工作效率之和）．
解答 解：甲的工作效率：$\frac{1}{a}$，乙的工作效率：$\frac{1}{b}$，
则甲、乙两人合做完成这项工程的天数是1÷（$\frac{1}{a}$+$\frac{1}{b}$）=$\frac{ab}{a+b}$．
故答案为：$\frac{ab}{a+b}$．
点评 此题考查列代数式，注意把工作总量看作单位1，掌握工作总量、工作效率、工作时间三者之间的关系，最后注意代数式的化简．
练习册系列答案
相关题目
20．
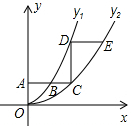如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2=$\frac{{x}^{2}}{4}$（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则$\frac{DE}{AB}$=（ ）
如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2=$\frac{{x}^{2}}{4}$（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则$\frac{DE}{AB}$=（ ）| A． | 2：1 | B． | $\sqrt{2}$：1 | C． | $\sqrt{5}$：1 | D． | 3：1 |
18．
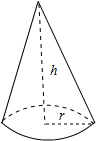如图，圆锥体的高h=2$\sqrt{3}$cm，底面圆半径r=2cm，则圆锥体的全面积为（ ）
如图，圆锥体的高h=2$\sqrt{3}$cm，底面圆半径r=2cm，则圆锥体的全面积为（ ）| A． | 4$\sqrt{3}$πcm2 | B． | 8πcm2 | C． | 12πcm2 | D． | （4$\sqrt{3}$+4）πcm2 |
5．若y-1与2-x成正比例，则下列说法正确的是（ ）
| A． | y是x的一次函数 | B． | y是x的正比例函数 | ||
| C． | y是x的函数但不是正比例函数 | D． | y不是x的函数 |
