题目内容
2.解下列方程组:(1)$\left\{\begin{array}{l}{5x+2y=8}\\{3x-y=7}\end{array}\right.$(用代入法)
(2)$\left\{\begin{array}{l}{3x-2y=8}\\{x+2y=16}\end{array}\right.$(用加减法)
(3)$\left\{\begin{array}{l}{x-2=2(y-1)}\\{2(x-2)+(y-1)=5}\end{array}\right.$
(4)$\left\{\begin{array}{l}{\frac{x+1}{3}=\frac{y+2}{4}}\\{\frac{x-3}{4}-\frac{y-3}{3}=\frac{1}{12}}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{5x+2y=8①}\\{3x-y=7②}\end{array}\right.$,
由②得:y=3x-7③,
把③代入①得:5x+6x-14=8,
解得:x=2,
把x=2代入③得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x-2y=8①}\\{x+2y=16②}\end{array}\right.$,
①+②得:4x=24,即x=6,
把x=6代入②得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=5}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{x-2y=0①}\\{2x+y=10②}\end{array}\right.$,
①+②×2得:5x=20,即x=4,
把x=4代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{4x-3y=2①}\\{3x-4y=-2②}\end{array}\right.$,
②×3-①×3得:-3y=-12,即y=4,
把y=4代入①得:x=$\frac{14}{3}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{14}{3}}\\{y=4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | 215÷23=212 | B. | (-x2)3=x6 | C. | 8-4÷8-2=64 | D. | x0=0 |
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |

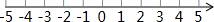 利用数轴,解一元一次不等式组:$\left\{\begin{array}{l}{x+4≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$.
利用数轴,解一元一次不等式组:$\left\{\begin{array}{l}{x+4≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$.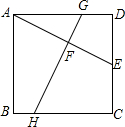 如图,正方形ABCD中,AB=4,E为BC的中点,F为AE的中点,过点F作GH⊥AE,分别交AB和CD于G、H,求GF的长,并求$\frac{GF}{GH}$的值.
如图,正方形ABCD中,AB=4,E为BC的中点,F为AE的中点,过点F作GH⊥AE,分别交AB和CD于G、H,求GF的长,并求$\frac{GF}{GH}$的值. 如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.